Задача 67739 Infx, , supx, верхний предел, нижний...
Условие
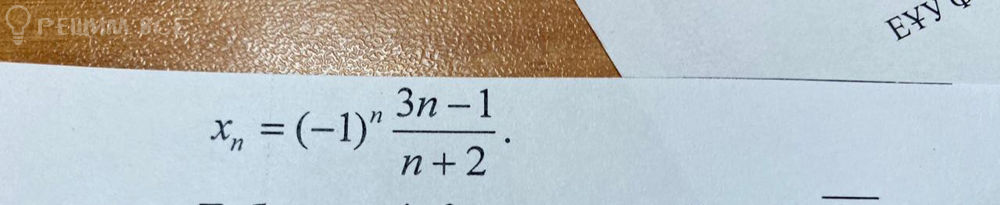
289
Решение
★
x_(1)=[m](-1)^1\cdot \frac{3\cdot 1-1}{1+2}[/m]
x_(1)=-2/3
n=2
x_(2)=[m](-1)^2\cdot \frac{3\cdot 2-1}{2+2}[/m]
x_(2)=5/4
n=3
x_(3)=[m](-1)^3\cdot \frac{3\cdot 1-1}{1+2}[/m]
x_(3)=-8/5
n=4
x_(4)=[m](-1)^4\cdot \frac{3\cdot 4-1}{4+2}[/m]
x_(4)=11/6
[m]\overline{lim}_{n → ∞}x_{n}=lim_{k → ∞ }(-1)^{2k+1}\frac{3\cdot (2k+1)-1}{2k+1+2}=-3[/m]
[m]\underline{lim}_{n → ∞}x_{n}=lim_{k → ∞ }(-1)^{2k}\frac{3\cdot 2k-1}{2k+2}=3[/m]
⇒
Последовательность предела не имеет