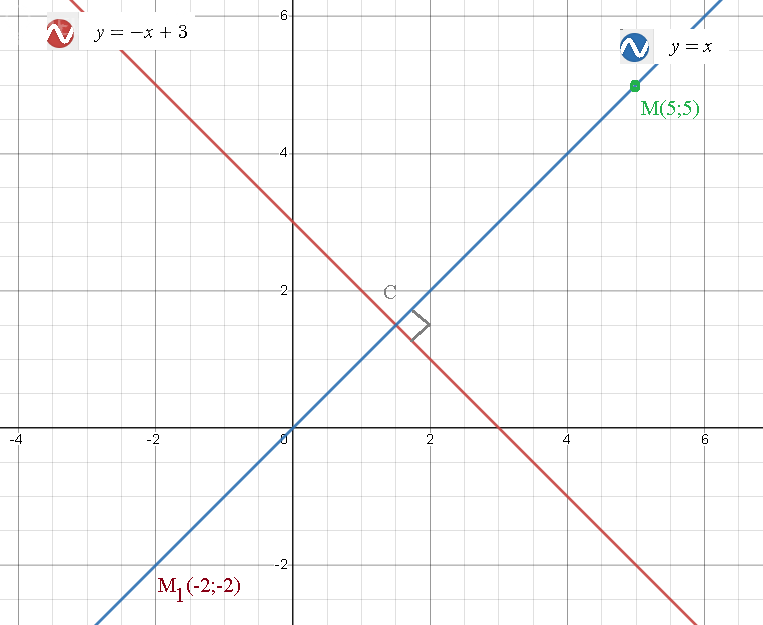
Задача 67406 Найти точку, симметричную точке М(5;5)...
Условие
Решение
Значит составляем уравнение такой прямой
x+y-3=0 ⇒ y=-x+3
k=-1
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
Значит, угловой коэффициент перпендикулярной прямой k=1
y=x+b - общий вид перпендикулярных прямых
Подставляем координаты точки М
5=5+b
b=0
y=x- уравнение прямой перпендикулярной данной.
Находим точку пересечения двух прямых
Решаем систему:
{y=x
{y=-x+3
x=-x+3
2x=3
x=1,5
y=1,5
Пусть это точка C (1,5; 1,5)
По свойству симметричных точек
МС=СМ_(1)
⇒
С- середина отрезка ММ_(1)
x_(C)=(x_(M)+x_(M_(1)))/2 ⇒ x_(M_(1))=2x_(C)-x_(M)=2*1,5-5=-2
y_(C)=(y_(M)+y_(M_(1)))/2 ⇒ y_(M_(1))=2x_(C)-x_(M)=2*1,5-5=-2
О т в е т. M_(1)(-2;-2)