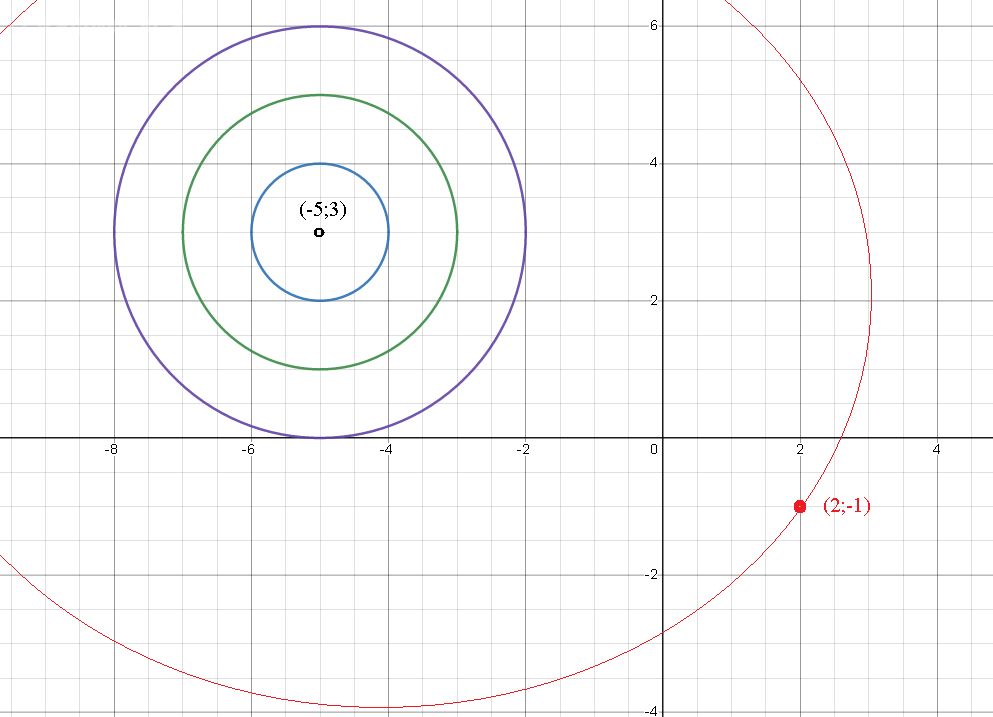
Задача 66928 1. Окружность с центром в точке А (-5;...
Условие
2. Напишите уравнение прямой, проходящей через начало ко- оринат и точку В (-2; 4). 
Решение
(x-(-5))^2+(y-3)^2=R^2 - уравнение окружности с центром в точке А
(x+5)^2+(y-3)^2=R^2
Таких окружностей бесчисленное множество
Так как по условию, окружность проходит через точку В, то это единственная окружность.
Подставим координаты точки В в уравнение и найдем R^2
(2+5)^2+(-1-3)^2=R^2 ⇒ 49+16=R^2
R^2=65
О т в е т.
(x+5)^2+(y-3)^2=65
2.
y=kx - общий вид уравнения прямой, проходящей через начало координат
Так как по условию нужна единственная прямая, которая проходит через точку
B(-2;4)
подставим координаты точки В в уравнение
4=k*(-2)
k=-2
y=-2x
О т в е т. y=-2x