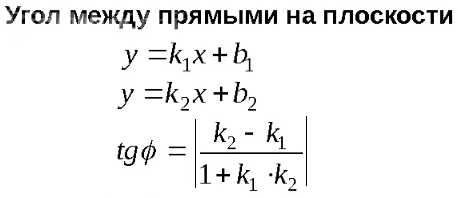Задача 66748 Найти уравнение прямой, проходящей...
Условие
Решение
k_(1)=4
Будем искать уравнение прямой в виде уравнения с угловым коэффициентом
Обозначим угловой коэффициент искомой прямой k_(2)
По условию искомая прямая образует угол 45 ° с данной прямой
По формуле:
[m]tgφ=|\frac{k_{2}−k_{1}}{1+k_{1}⋅k_{2}}|[/m]
[m]tg45°=|\frac{k_{2}−4}{1+4⋅k_{2}}|[/m] ⇒
[m]1=|\frac{k_{2}−4}{1+4⋅k_{2}}|[/m] ⇒
[m]4k_{2}+1=k_{2}−4[/m] или [m]4k_{2}+1=-(k_{2}−4)[/m]
[m]k_{2}=−\frac{5}{3}[/m] или [m]k_{2}=\frac{3}{5}[/m]
Уравнение прямой принимает вид
[m]y=−\frac{5}{3}x+m[/m] или [m]y=\frac{3}{5}x+n[/m]
Чтобы найти m и n подставим координаты точки, через которую проходит эта прямая.
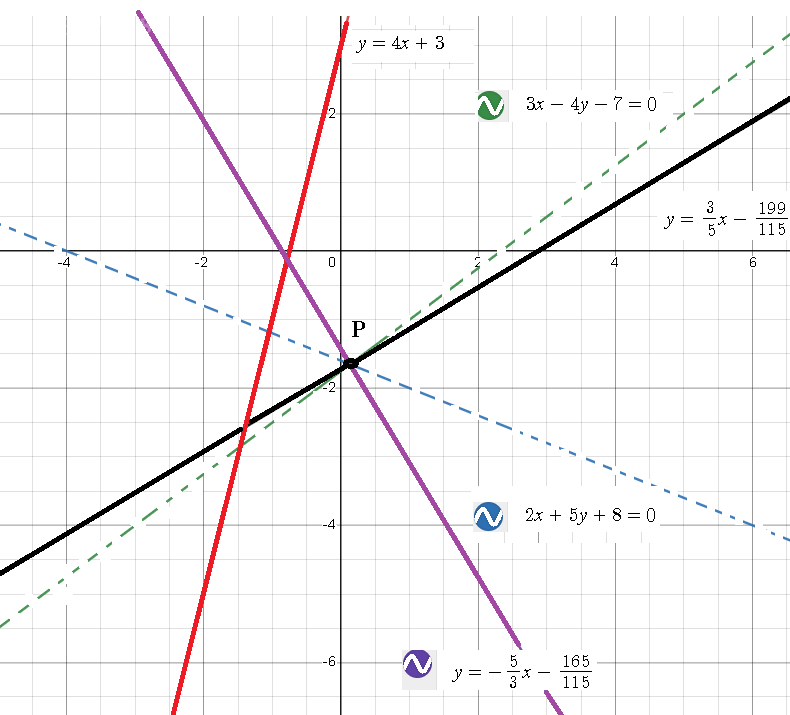
По условию такой точкой является пересечения прямых 2x + 5y + 8 = 0 и 3x–4y–7 = 0
Решаем систему уравнений:
{2x+5y+8=0
{3x–4y–7=0
Умножаем первое уравнение на 4, второе на 5
{8x+20y+32=0
{15x–20y–35=0
Складываем
23x–3=0
x=3/23
5y=-2x-8
5y=-2*(3/23)-8
y=-190/115
P(3/23; –190/115)
Подставляем координаты точки Р в уравнение [m]y=−\frac{5}{3}x+m[/m]
[m]-\frac{190}{115}=−\frac{5}{3}\cdot \frac{3}{23}+m[/m] ⇒[m] m=-\frac{165}{115}[/m] ⇒ [m] m=-\frac{165}{115}[/m]
Подставляем координаты точки Р в уравнение [m]y=\frac{3}{5}x+n[/m]
[m]-\frac{190}{115}=\frac{3}{5}\cdot \frac{3}{23}+n[/m]⇒ [m] n=-\frac{199}{115}[/m]
О т в е т.
[m]y=−\frac{5}{3}x-\frac{165}{115}[/m] или [m]y=\frac{3}{5}x-\frac{199}{115}[/m]