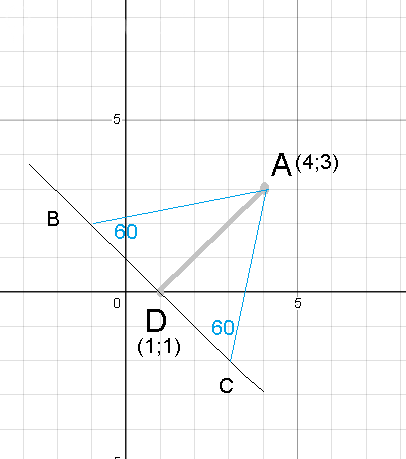
Задача 66610 26, Bсe углы треугольника равны 60....

6360c3cefbda3e2dde2ea57a

01.11.2022 10:03:00

26, Bсe углы треугольника равны 60. Даны — вершина А(4,3) и точка: Д(1,1) пересечения опущенной из А высоты и стороны ВС. Составить уравнения сторон треугольника и найти координаты остальных вершин.

5f3ea7e3faf909182968ddd9

01.11.2022 12:48:52

★

Уравнение AD как прямой, проходящей через две точки:

(x-4)/(1-4)=(y-3)/(1-2) ⇒ 2x-3y+1=0

у=(2/3)х+(1/3)

k_(AD)=2/3

AD ⊥ BC ⇒ k_(AD)*k_(BC)=-1

k_(BC)=-3/2

Уравнение прямой ВС имеет вид

y=(-3/2)*x+b

Чтобы найти b подставляем координаты точки D

[b]1[/b]=(-3/2)*[b]1[/b]+b

b=5/2

y=(-3/2)*x+(5/2) - уравнение прямой BC



Используем углы в 60 ° ( cм формулу в первом столбце)


tg ∠ ABC=(k_(BC)-k_(AB))/(1-k_(BC)*k_(AB))

∠ ABC=60 °

k_(BC)=-3/2

⇒

k_(AB)=

Общий вид уравнений прямых, составляющего со стороной ВС угол в 60 °


y=k_(AB)+b_(1)

Чтобы найти b_(1) подставляем координаты точки А



Аналогично

tg ∠ ACВ=(k_(BC)-k_(AС))/(1-k_(BC)*k_(AС))

∠ ACВ=60 °

k_(BC)=-3/2

⇒

k_(AС)=

Общий вид уравнений прямых, составляющего со стороной ВС угол в 60 °

y=k_(AС)+b_(2)

Чтобы найти b_(2) подставляем координаты точки B