Задача 65941 .Составить уравнения сторон квадрата,...
Условие
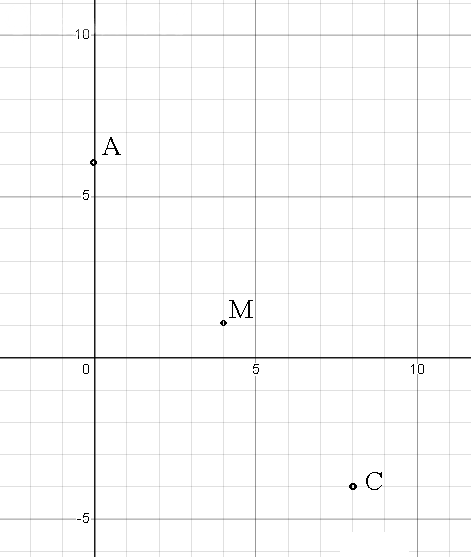
известны координаты вершины A(0, 6) и уравнения
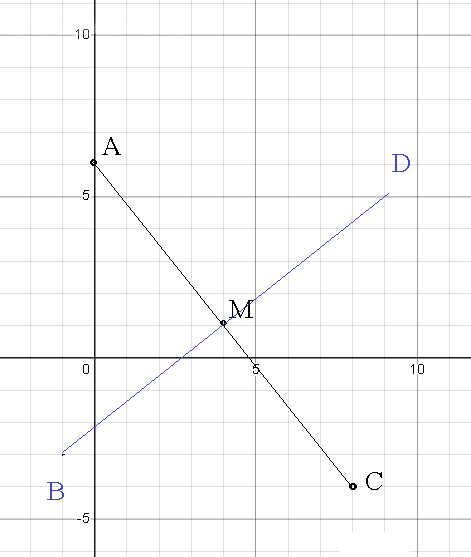
диагоналей AC:
5x+4y-24=0 , BD:
4x-5y-11=0 .
Решение
BD:4x–5y–11=0 .
Диагонали квадрата пересекаются в точке М
Найдем координаты точки М, решаем систему уравнений:
[m]\left\{\begin {matrix} 5x+4y–24=0\\4x–5y–11=0 \end {matrix}\right.[/m] ⇒
Решаем систему способом сложения.
Умножаем первое уравнение на 5, второе на 4:
[m]\left\{\begin {matrix} 25x+20y–120=0\\16x–20y–44=0 \end {matrix}\right.[/m]
и складываем ( т.е заменяем одно из уравнений суммой этих уравнений):
[m]\left\{\begin {matrix} 25x+20y–120=0\\41x–164=0 \end {matrix}\right.[/m]
[m]\left\{\begin {matrix} 25\cdot 4+20y–120=0\\x=4 \end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix} y=1\\x=4 \end {matrix}\right.[/m]
M(4:1)
M - середина АС
Применяем формулы для нахождения координат середины отрезка
Координаты точки M как середины АС
[m]x_{M}=\frac{x_{A}+x_{C}}{2}[/m] ⇒ [m]x_{C}=2x_{M}-x_{A}=2\cdot 4-0=8[/m]
[m]y_{M}=\frac{y_{A}+y_{C}}{2}[/m] ⇒ [m]y_{C}=2y_{M}-y_{A}=2\cdot 1-6=-4[/m]
Применяем свойства диагоналей квадрата:
АМ=МС=ВМ=МD
АМ=sqrt((4-0)^2+(1-6)^2)=sqrt(16+25)=sqrt(41)
ВМ=sqrt((x_(B)-0)^2+(y_(B)-6)^2) ⇒
sqrt((x_(B)-0)^2+(y_(B)-6)^2) =sqrt(41)
Возводим в квадрат:
(x_(B)-0)^2+(y_(B)-6)^2=41
Так как точка B принадлежит прямой BD, то её координаты удовлетворяют уравнению этой прямой:
4x_(В)–5y_(В)–11=0 .
Решаем систему двух уравнений, находим координаты точки B
{(x_(B)-0)^2+(y_(B)-6)^2=41
{4x_(В)–5y_(В)–11=0 .
Аналогично находим координаты точки D
Чтобы составить уравнения сторон применяем формулу уравнения прямой, проходящей через две точки