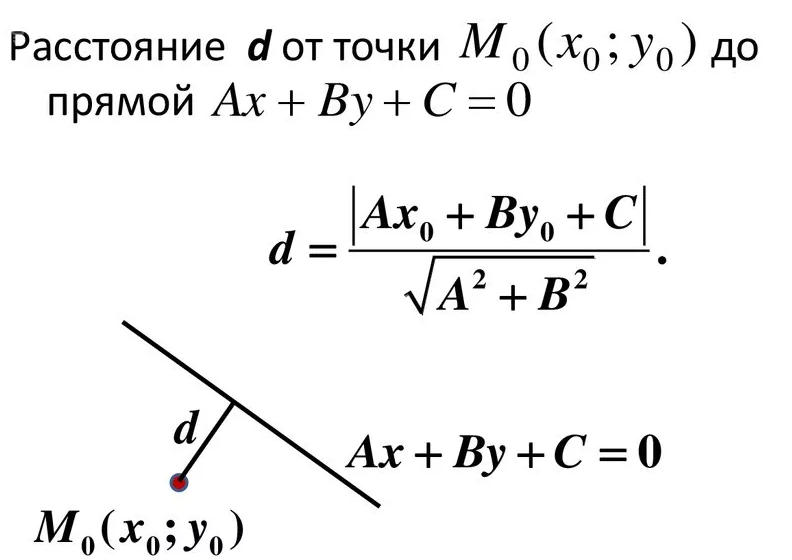Задача 65824 1. Составить уравнение прямой,...
Условие
а) Записать его в общем виде, уравнением с угловым коэффициентом, уравнением в отрезках, нормальным уравнением.
б) Определить:
- длину перпендикуляра, опущенного из начала координат на эту прямую,
- расстояние от точки (1,2) до этой прямой,
- угол между этой прямой и прямой x+y-6=0
2. Составить уравнение прямой, проходящей через точку пересечения прямых: 2x-5y+11=0
5x+2y-16=0 и параллельно оси ординат.
Решение
a)
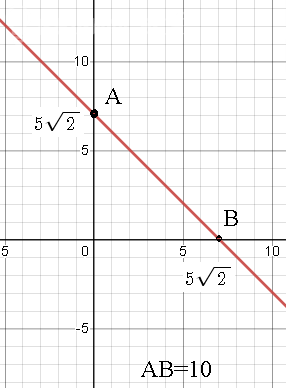
Отрезки, отсекаемые на осях координат- катеты прямоугольного равнобедренного треугольника
AOB с гипотенузой AB=10 ( см. рис.)
Значит, координаты точек А(0; 5sqrt(2)); B(5sqrt(2);0).
Составляем уравнение прямой, проходящей через точки А и В
Уравнение прямой в отрезках:
[m]\frac{x}{5\sqrt{2}}+\frac{y}{5\sqrt{2}}=1[/m]
⇒
[m]x+y=5\sqrt{2}[/m]- общее уравнение прямой вида: [m]ax+by=c[/m] или
[m]x+y- 5\sqrt{2}=0[/m] вида: [m]ax+by+c=0[/m]
[m]y=-x+5\sqrt{2}[/m] - уравнение прямой с угловым коэффициентом вида y=kx+b
Нормальное уравнение прямой имеет вид:
[m] xcos α+ysin α- p=0[/m]
[m]x\cdot \frac{1}{\sqrt{2}}+y\cdot \frac{1}{\sqrt{2}}-5=0[/m] - нормальное уравнение искомой прямой
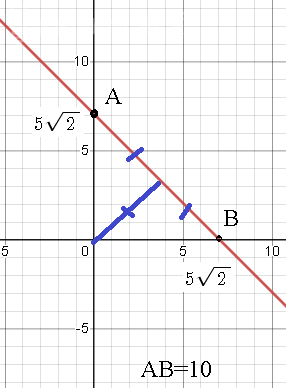
б) длина перпендикуляра, опущенного из начала координат О на АВ
это высота прямоугольного треугольника из вершины прямого угла на гипотенузу.
Эта высота равна половине гипотенузы..
О т в е т [b]5[/b]
Расстояние от точки (1;2) до этой прямой ( см формулу в скрине):
[m]d=\frac{|1+2-5\sqrt{2}|}{\sqrt{1^2+1^2}}[/m]
[m]d=\frac{|3-5\sqrt{2}|}{\sqrt{2}}[/m]
Прямые
[m]x+y-5\sqrt{2}=0[/m] и [m]x+y-6=0[/m]- параллельны.
Угол между ними 0 °
Находим координаты точки пересечения прямых.
Решаем систему:
{2x-5y+11=0
{5x+2y-16=0
Умножаем первое уравнение на 2, второе на 5
{4x-10y+22=0
{25x+10y-80=0
Складываем:
29х-58=0
[b]
х=2[/b]
2*2-5y+11=0
-5y=-15
y=-3
M(2;-3) - точка пересечения прямых
х=2 - уравнение прямой, проходящей через точку М [i]параллельно оси ординат[/i]