Задача 64539 1. Найти острый угол между прямыми 3x –...
Условие
2. Составить уравнение прямой в полярных координатах, если известно, что она проходит через точку M(4 ; p/4)и наклонена к полярной оси под углом p/6 .
3. Дан треугольник с вершинами в точках A(2; –3), B(1; 6), C(–6; 3) . Найти координаты центра описанной около треугольника окружности.
4. Какая из прямых 3x – 4y + 5 = 0 и 2x + 7y – 1 = 0 отсекает на оси ординат отрезок большей длины?
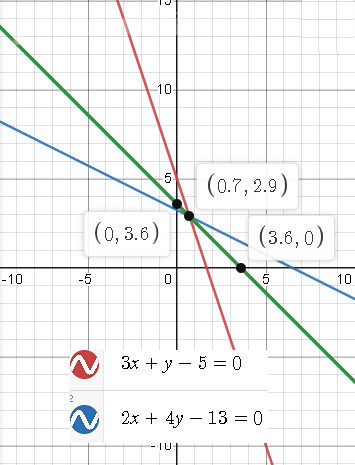
5. Через точку пересечения прямых 3x + y – 5 = 0 и 2x + 4y –13 = 0 провести прямую (не совпадающую с данными), отсекающую на осях равные отрезки и написать её уравнение.
Решение
Уравнения общего вида
3x – 4y + 8 = 0 и 2x – 6y =10 задают прямые.
Геометрический смысл коэффициентов уравнений: - координаты направляющих векторов
vector{n_(1)}=(3;-4) и vector{n_(2)}=(2;-6)
Угол между прямыми ( см. формулу в скрине)
Oбозначим
vector{n_(1)}=vector{a}
vector{n_(2)}= vector{b}
И найдем косинус угла между векторами, пользуясь определением скалярного произведения
2. Составить уравнение прямой в полярных координатах, если известно, что она проходит через точку M(4 ; p/4)и наклонена к полярной оси под углом p/6 .
Уравнение прямой с угловым коэффициентом [i]в декартовых координатах[/i] имеет вид:
y=kx+b
[i]Геометрический смысл углового коэффициента [/i]k
k=tg α , α - угол, который образует прямая с положительным направлением оси Ох
[u]По условию[/u] прямая наклонена к полярной оси под углом[b] π/6 .[/b]
В полярных координатах полярная ось совпадает с осью Ох
k=tg (π/6)=sqrt(3)/3
Значит уравнение прямой y=(sqrt(3)/3)x + b
Чтобы найти b подставляем координаты точки М
M(4 ; p/4)- полярные координаты точки.
Декартовы координаты:
x=4*cos(π/4)=4*(sqrt(2)/2)=2sqrt(2)
y=4*sin(π/4)=4*(sqrt(2)/2)=2sqrt(2)
y=(sqrt(3)/3)x + b
2sqrt(2)=(sqrt(3)/3)*(2sqrt(2))+b
b=2sqrt(2)*(3-sqrt(3))/3
Уравнение прямой в декартовых координатах
y=(sqrt(3)/3)x +2sqrt(2)*(3-sqrt(3))/3
Переходим к полярным координатам:
x= ρ *cos θ
y= ρ *sin θ
ρ *sin θ
ρ *sin θ=(sqrt(3)/3)* ρ *cos θ +2sqrt(2)*(3-sqrt(3))/3 ⇒ ρ *sin θ-(sqrt(3)/3)* ρ *cos θ =2sqrt(2)*(3-sqrt(3))/3
выражаем ρ =(2sqrt(2)*(3-sqrt(3))/3)/( sin θ-(sqrt(3)/3)* cos θ )
Это и есть уравнение окружности в полярных координатах
3. Дан треугольник с вершинами в точках A(2; –3), B(1; 6), C(–6; 3) .
O(x_(o);y_(o)
АO=BO=CO
[m]AO=\sqrt{(x_{o}-2)^2+(y_{o}-(-3))^2}[/m]
[m]BO=\sqrt{(x_{o}-1)^2+(y_{o}-6)^2}[/m]
[m]CO=\sqrt{(x_{o}-(-6))^2+(y_{o}-3)^2}[/m]
[m]\sqrt{(x_{o}-2)^2+(y_{o}-(-3))^2}=\sqrt{(x_{o}-1)^2+(y_{o}-6)^2}[/m]
[m]\sqrt{(x_{o}-1)^2+(y_{o}-6)^2}=\sqrt{(x_{o}-(-6))^2+(y_{o}-3)^2}[/m]
Решаем систему и находим координаты центра окружности
4. Какая из прямых 3x – 4y + 5 = 0 и 2x + 7y – 1 = 0 отсекает на оси ординат отрезок большей длины?
Прямая, заданная уравнением: 3x – 4y + 5 = 0,
пересекает ось Оу в точке x=0
-4y+5=0 ⇒ y=5/4
Значит прямая отсекает на оси ординат отрезок длины (5/4)
Прямая, заданная уравнением: 2x + 7y – 1 = 0,
пересекает ось Оу в точке x=0
7y-1=0 ⇒ y=1/7
Прямая, заданная уравнением: 2x + 7y – 1 = 0,отсекает на оси ординат отрезок длины (1/7)
5/4 > 1/7
Прямая, заданная уравнением: 3x – 4y + 5 = 0, отсекает на оси ординат отрезок большей длины
5. Находим координаты точки пересечения прямых
3x + y – 5 = 0 и 2x + 4y –13 = 0
Решаем систему уравнений:
{3x + y – 5 = 0 ( умножаем на (-2))
{ 2x + 4y –13 = 0 ( умножаем на 3
{-6x-2y+10=0
{6x+12y-39=0
Складываем 10y-29=0
y=2,9
x=0,7
Если искомая прямая отсекает на осях координат равные отрезки, то значит прямая проходит через точки вида
(0;а) и (а;0)
или
(0;а) и (-а;0)
Составляем уравнение прямой, проходящей через точки
(0,7;2,9)
(0;а)
(а;0)
Будем находить уравнение в виде:
y=kx+b
Подставляем координаты точки (0;а)
a=0+b
b=a
Подставляем координаты точки (a;0)
0=ka+a
k=-1
y=-x+a
Подставляем координаты точки (0,7;2,9)
2,9=-0,7+a
a=3,6
О т в е т. y=-x+3,6
См. рис.
Уравнение второй прямой составляйте самостоятельно