Задача 64293 Дана функция f(x) = ln(-2 · x^2 - 2 · x...
Условие
f(x) = ln(-2 · x^2 - 2 · x + 8).
Найдите f'(-2).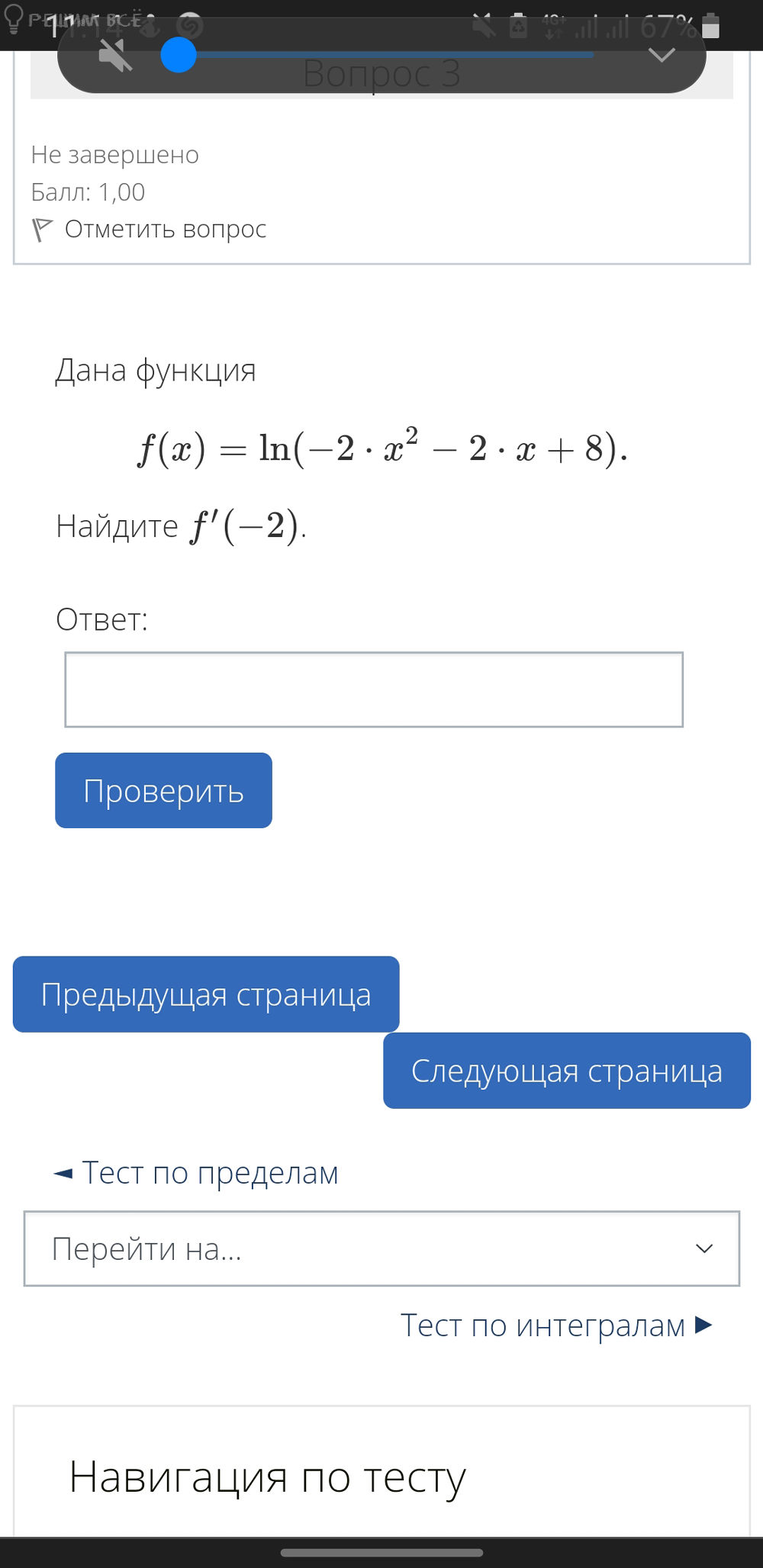
математика ВУЗ
442
Решение
★
[m](lnx)`=\frac{1}{x}[/m]
По правилу вычисления производной сложной функции
[m](ln(u(x)))`=\frac{1}{u(x)}\cdot u`(x)[/m]
[m]f(x)=ln(-2x^2-2x+8)[/m]
[m]u=-2x^2-2x+8[/m]
[m]f`(x)=\frac{1}{(-2x^2-2x+8)}\cdot (-2x^2-2x+8)`[/m]
[m]f`(x)=\frac{1}{(-2x^2-2x+8)}\cdot (-4x-2)[/m]
[m]f`(x)=\frac{(-4x-2)}{(-2x^2-2x+8)}[/m]
[m]f`(x)=\frac{4x+2}{2x^2+2x-8}[/m]
[m]f`(-2)=\frac{4\cdot (-2)+2}{2\cdot (-2)^2+2\cdot (-2)-8}[/m] считайте...