Задача 63713 Найти уравнение прямой, проходящую через...

623777bb3a946c784f3aac3c

20.03.2022 21:52:26

Найти уравнение прямой, проходящую через точку М(-3;-4) и параллельной прямой х-3у-5=0

5f3ea7e3faf909182968ddd9

20.03.2022 22:00:43

★

Прямая задана общим уравнением вида

ax+by+c=0

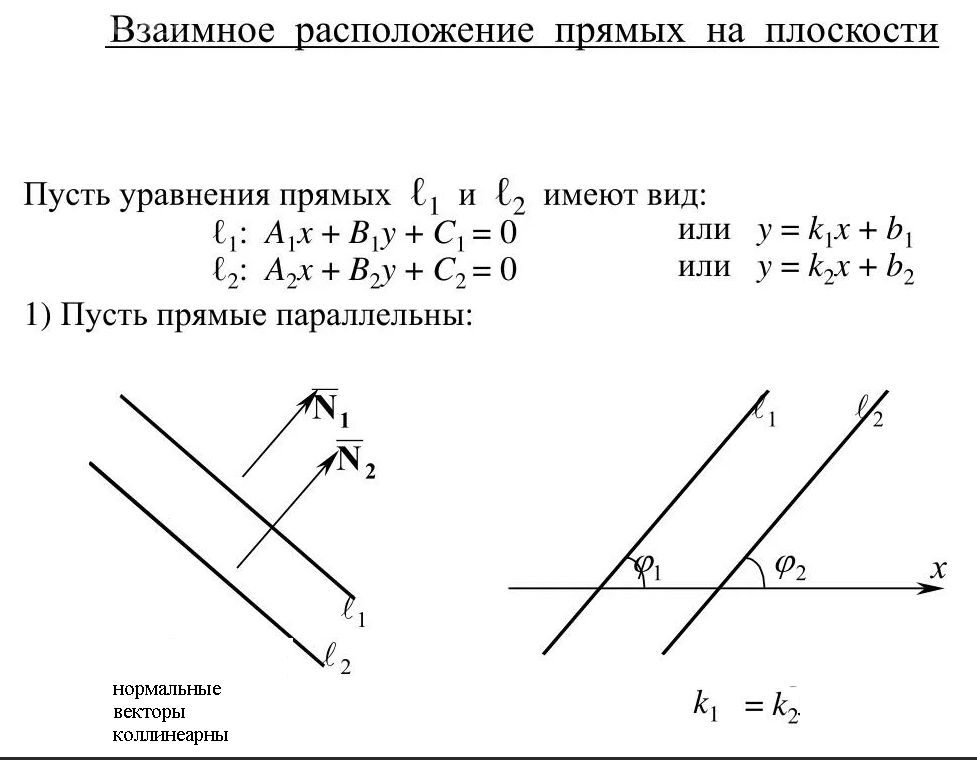
Прямые параллельны, если их направляющие векторы vector{n}=(a;b) коллинеарны.

Поэтому уравнение прямой, параллельной данной и имеющей такой же нормальный вектор имеет вид:
x-3y+c=0

Подставляем координаты точки М и находим с

-3-3*(-4)+с=0
с=-9

О т в е т. x-3y-9=0