Задача 63373 ...
Условие
A) lim [x(ln(x + 1) - ln x)] as x → +∞
B) lim [cos x - cos^2 x / x^2] as x → 0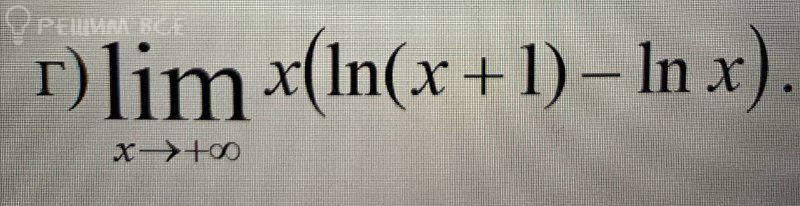
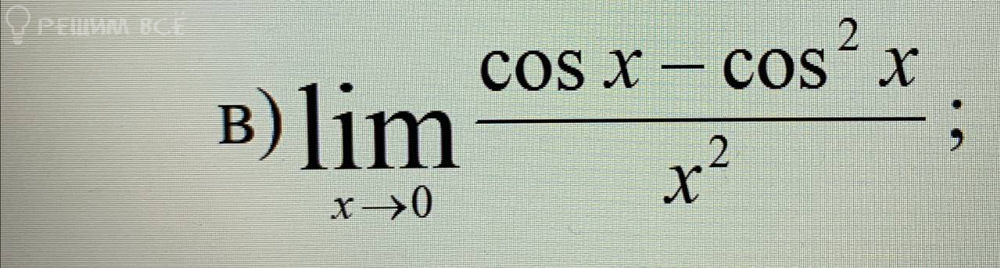
Решение
г)
ln(x+1)-lnx=ln((x+1)/x)=ln(1+(1/x))
x*(ln(x+1)-lnx)=x*ln(1+(1/x))=ln(1+(1/x))^(1/x)
lim_(x → ∞ )x*(ln(x+1)-lnx)=lim_(x → ∞ )ln(1+(1/x))^(x)=
знак предела и знак непрерывной функции ( у наc ln) можно менять местами:
=ln lim_(x → ∞ )(1+(1/x))^(x)=
второй замечательный предел:
=ln lim_(x → ∞ )[b]([/b](1+(1/x))^(x)=lne=1
в)
[m]lim_{x →0}\frac{cosx-cos^2x}{x^2}=lim_{x →0}\frac{cosx\cdot (1-cosx)}{x^2}=[/m]
Применяем формулу:
[r][m]1-cos2 α =2sin^2 α [/m][/r]
[m]lim_{x →0}\frac{cosx\cdot 2sin^2\frac{x}{2}}{x^2}=2\cdot lim_{x →0} cosx\cdot lim_{x →0}\frac{sin\frac{x}{2}}{2\frac{x}{2}} \cdot lim_{x →0}\frac{sin\frac{x}{2}}{2\frac{x}{2}}=2\cdot \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{2} [/m]
