Задача 63135 нужно решить предел...
Условие
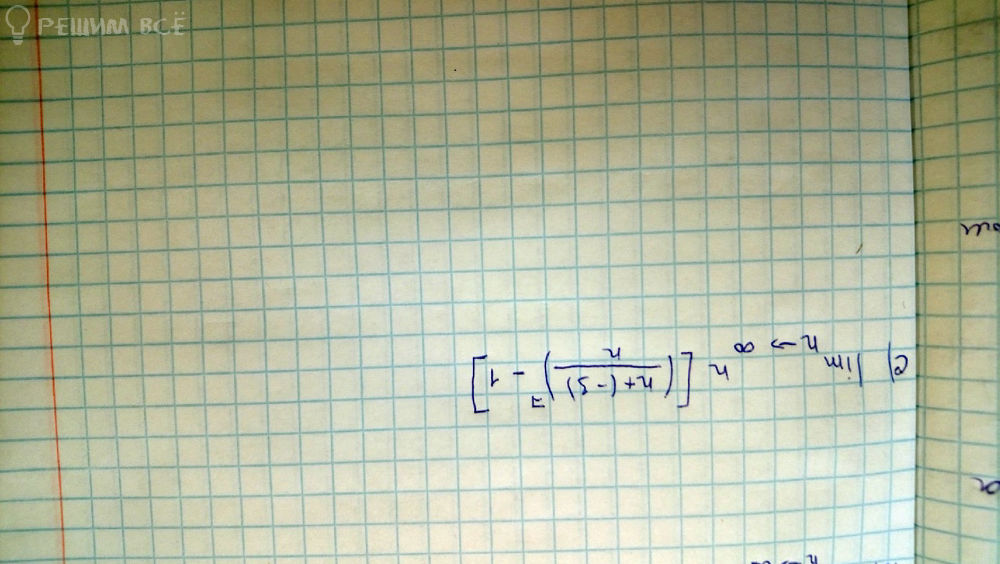
математика ВУЗ
336
Решение
★
по формуле бинома:
[m](1+x)^7=1+7x+21x^2+35x^3+35x^4+21x^5+7x^6+x^7[/m]
[m](\frac{n+(-3)}{n})^7-1=[/m]
[m]=(1+\frac{(-3)}{n})^7-1=1+7\cdot\frac{(-3)}{n}+21\cdot (\frac{(-3)}{n})^2+35\cdot (\frac{(-3)}{n})^3+35\cdot (\frac{(-3)}{n})^4+21\cdot (\frac{(-3)}{n})^5+7\cdot (\frac{(-3)}{n})^6+ (\frac{(-3)}{n})^7-1 [/m]
Тогда
[m]lim_{n → ∞ } n\cdot ((\frac{n+(-3)}{n})^7-1)=[/m]
[m]=lim_{n → ∞ } n\cdot (7\cdot\frac{(-3)}{n}+21\cdot (\frac{(-3)}{n})^2+35\cdot (\frac{(-3)}{n})^3+35\cdot (\frac{(-3)}{n})^4+21\cdot (\frac{(-3)}{n})^5+7\cdot (\frac{(-3)}{n})^6+ (\frac{(-3)}{n})^7)=[/m]
=7+0+0+0+0+0+0=7[/m]