Задача 62776 Запишите уравнение прямой, проходящей...

Clay

21 января 2022 г. в 18:33

Запишите уравнение прямой, проходящей через точку P(−3;5) на одинаковом расстоянии от точек A(−4;−1) и B(3;2) .

exponenta

21 января 2022 г. в 19:56

★

Пусть уравнение прямой имеет вид:
$ax+by+c=0$

Тогда расстояние от точки А(–4;–1) до этой прямой:

$d_{1}=\frac{|a\cdot (-4)+b\cdot (-1)+c|}{\sqrt{a^2+b^2}}$

Тогда расстояние от точки B(3;2) до этой прямой:

$d_{2}=\frac{|a\cdot 3+b\cdot 2+c|}{\sqrt{a^2+b^2}}$


По требованию задачи:

1) $d_{1}=d_{2}$ ⇒ $|a\cdot (-4)+b\cdot (-1)+c|=|a\cdot 3+b\cdot 2+c|$


2) прямая $ax+by+c=0$ проходит через точку Р(–3;5)

$a\cdot (-3)+b\cdot 5+c=0$ ⇒ $-3a+5b+c=0$


Решаем систему двух уравнений и находим а и b:

$\left\{\begin {matrix} |a\cdot (-4)+b\cdot (-1)+c|=|a\cdot 3+b\cdot 2+c|\\-3a+5b+c=0\end {matrix}\right.$ ⇒


$\left\{\begin {matrix} a\cdot (-4)+b\cdot (-1)+c=a\cdot 3+b\cdot 2+c\\-3a+5b+c=0\end {matrix}\right.$ или $\left\{\begin {matrix}a\cdot (-4)+b\cdot (-1)+c=-a\cdot 3-b\cdot 2-c\\-3a+5b+c=0\end {matrix}\right.$


$\left\{\begin {matrix} -4a-b=3a+2b\\-3a+5b+c=0\end {matrix}\right.$ или $\left\{\begin {matrix}-a+b+2c=0\\-3a+5b+c=0\end {matrix}\right.$ умножим второе уравнение на 2

$\left\{\begin {matrix} b=-\frac{7}{3}a\\c=\frac{44}{3}\end {matrix}\right.$ или $\left\{\begin {matrix}-a+b+2c=0\\-6a+10b+2c=0\end {matrix}\right.$ вычитаем из одного второе

$\left\{\begin {matrix} b=-\frac{7}{3}a\\c=\frac{44}{3}\end {matrix}\right.$ или $\left\{\begin {matrix}- \frac{9}{5}b+b+2c=0\Rightarrow c=\frac{2}{5}b\\a=\frac{9}{5}b\end {matrix}\right.$

О т в е т.
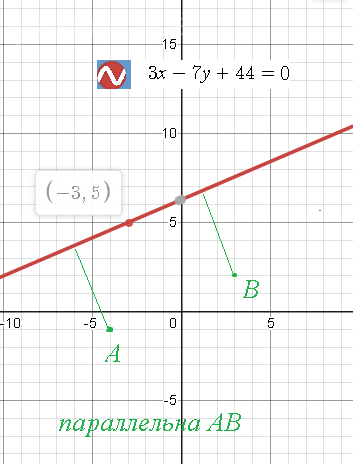
1) $ax+(-\frac{7}{3}a)y+\frac{44}{3}=0$ ⇒$3x-7y+44=0$

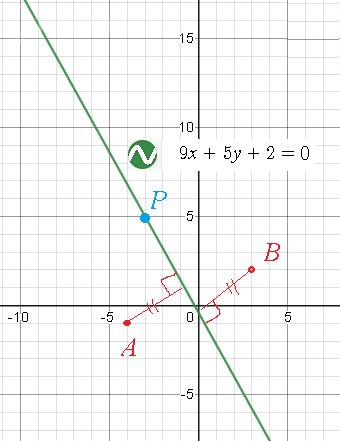
2)$\frac{9}{5}bx+by+\frac{2}{5}b=0$ ⇒ $9x+5y+2=0$