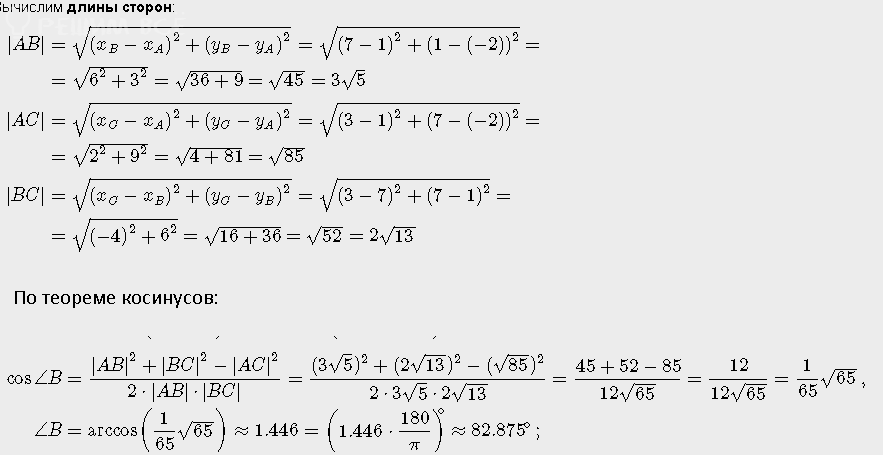Задача 62117 Даны вершины треугольника ABC. Найти: а)...

61b5dba63573e63cc28dc88b

12.12.2021 14:25:20

Даны вершины треугольника ABC. Найти: а) уравнение стороны AB; б) уравнение высоты CH и ее длину; в) уравнение медианы AM и ее длину; г) точку пересечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину C параллельно стороне AB; е) внутренний угол В треугольника АВС
A(1;-2); B(7;1); C(3,7)

5f3ea7e3faf909182968ddd9

12.12.2021 19:10:09

★

a) см. скрин

б) Высота CH перпендикулярна прямой АВ.

Произведение угловых коэффициентов перпендикулярных прямых равно (-1)

k_(AB)*k_(CH)=-1

k_(CH)=-2

Общий вид прямых перпендикулярных АВ:

y=-2x+b

Подставляем координаты точки С (3;7)

х=3;у=7

7=-2*3+b

b=13

О т в е т. y=-2x+13


в)

Находим координаты точки М - середины ВС

[m]x_{M}=\frac{x_{B}+x_{C}}{2}=\frac{7+3}{2}=5[/m]

[m]y_{M}=\frac{y_{B}+y_{C}}{2}=\frac{1+7)}{2}=4[/m]


Составляем уравнение медианы АМ как прямой, проходящей через две точки:

Уравнение прямой, проходящей через две точки
A (x_(A);y_(A)) и M (x_(M);y_(M)) и имеет вид:

[m]\frac{x-x_{A}}{x_{M}-x_{A}}=\frac{y-y_{A}}{y_{M}-y_{A}}[/m]

A(1;-2)
M(5;4)


[m]\frac{x-1}{5 - 1}=\frac{y-(-2)}{4 -(-2)}[/m]

[m]\frac{x-1}{4}=\frac{y+2}{6}[/m]

[m]6(x-1)=4(y+2)[/m]

[b]6x-4y-14=0[/b]

[b]3x-2y-7=0[/b] - уравнение медианы АМ


г)

Решаем систему уравнений:

[m]\left\{\begin {matrix}y=-2x+13\\3x-2y-7=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}y=-2x+13\\3x-2(-2x+13)-7=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}y=-2x+13\\7x=33\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}y=-2\cdot \frac{33}{7}+13\\x=\frac{33}{7}\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}y= \frac{25}{7}\\x=\frac{33}{7}\end {matrix}\right.[/m]


О т в е т. ([m]\frac{33}{7};\frac{25}{7}[/m])

д) См. скрин 1


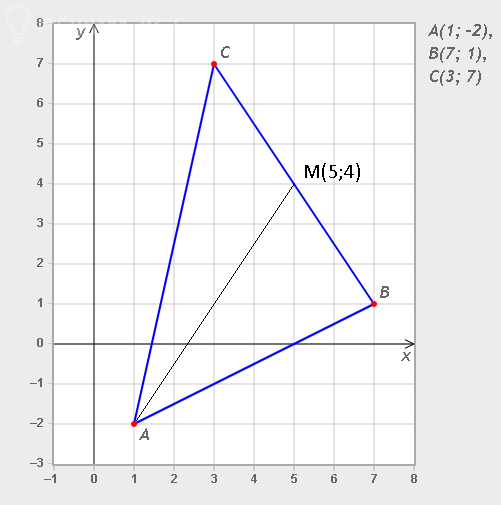
е) См. скрин 2