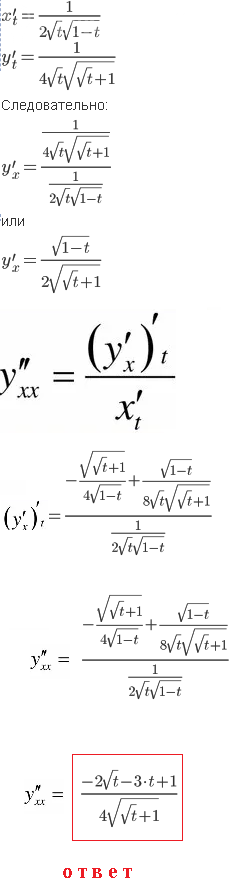Задача 61880 Вычислить [m]\frac{d^2y}{dx^2}[/m] для...

61a4b568b8fa7b3fbd3fe6f3

29.11.2021 21:39:41

Вычислить [m]\frac{d^2y}{dx^2}[/m] для функции y(x), заданной параметрически:
[m]x = \arcsin \sqrt{t}, y = \sqrt{1 + \sqrt{t} }[/m]

5f3ea7e3faf909182968ddd9

30.11.2021 14:24:58

★

[m]y`_{x}=\frac{y`_{t}}{x`_{t}}[/m]

[m]x`_{t}=(arcsin\sqrt{t})`_{t}=\frac{1}{\sqrt{1-(\sqrt{t})^2}}\cdot (\sqrt{t})`_{t}=\frac{1}{\sqrt{1-t}}\cdot \frac{1}{2\sqrt{t}}=\frac{1}{2\sqrt{(1-t)\cdot t}}[/m]


[m]y`_{t}=(\sqrt{1+\sqrt{t}})`_{t}=\frac{1}{2\sqrt{1+\sqrt{t}}}\cdot (1+\sqrt{t})`_{t}=\frac{\frac{1}{2\sqrt{t}}}{2\sqrt{1+\sqrt{t}}}=\frac{1}{4\sqrt{\sqrt{t}+t}}[/m]


[m]y``_{xx}=\frac{y``_{tt}\cdot x`_{t}-y`_{t}\cdot x``_{tt}}{x`_{t}}[/m]


[m]x``_{tt}=(x`_{t})`_{t}=(\frac{1}{2\sqrt{(1-t)\cdot t}})`_{t}=\frac{1}{2}\cdot ((1-t)\cdot t)^{-\frac{1}{2}})`_{t}=\frac{1}{2}\cdot (-\frac{1}{2})\cdot ((1-t)\cdot t)^{-\frac{3}{2}})\cdot ((1-t)\cdot t)`_{t}=-\frac{1}{4}\cdot \frac{1-2t}{\sqrt{(1-t)^3\cdot t^3}}[/m]


[m]y``_{tt}=(y`_{t})`_{t}=(\frac{1}{4\sqrt{\sqrt{t}+t}})`_{t}=\frac{1}{4}\cdot ((\sqrt{t}+t)^{-\frac{1}{2}})`_{t}=\frac{1}{4}\cdot (-\frac{1}{2})\cdot (\sqrt{t}+t)^{-\frac{3}{2}})\cdot (\sqrt{t}+t)`_{t}=-\frac{1}{8}\cdot \frac{\frac{1}{2\sqrt{t}}+1}{\sqrt{(\sqrt{t}+t)^3}}[/m]


[m]y``_{xx}=\frac{-\frac{1}{8}\cdot \frac{\frac{1}{2\sqrt{t}}+1}{\sqrt{(\sqrt{t}+t)^3}}\cdot \frac{1}{2\sqrt{(1-t)\cdot t}}-(-\frac{1}{4})\cdot \frac{1-2t}{\sqrt{(1-t)^3\cdot t^3}}\cdot\frac{1}{4\sqrt{\sqrt{t}+t}} }{(\frac{1}{2\sqrt{(1-t)\cdot t}})^3}[/m]

Упрощаем
[m]y``_{xx}=\frac{-2t-3t+1}{4(\sqrt{\sqrt{t}+1})^3}[/m]


О т в е т.
[m]y``_{xx}=y``_{xx}=\frac{-2t-3t+1}{4(\sqrt{\sqrt{t}+1})^3}[/m]


Второй способ

[m]y`_{x}=\frac{y`_{t}}{x`_{t}}[/m]


[m]y`_{x}=\frac{\sqrt{1-t}}{2\sqrt{\sqrt{t}+1}}[/m]


[m]y``_{xx}=\frac{(y`_{x})`_{t}}{x`_{t}}[/m]


[m]y``_{xx}=\frac{(\frac{\sqrt{1-t}}{2\sqrt{\sqrt{t}+1}})`_{t}}{\frac{1}{2\sqrt{(1-t)\cdot t}}}=...[/m]