Задача 60953 Можете решить 5 заданий (можно 3-4...
Условие

Решение
Испытание состоит в том что четыре книги расставляют на 4 места.
Это можно сделать
4! =1*2*3*4=24 способами
n=24
Событие A -" 4 тома расположены в порядке 1,2,3,4 или 4,3,2.1@
Это два способа
m=2
По формуле классической вероятности
p(A)=m/n=2/24=1/12
3.
Предположим, что один человек сел на одно из пяти мест.
n=5
Тогда для выбора места для второго человека есть 2 способа ( справа или слева от сидящего)
m=2
p=2/5 - вероятность того, что два человека будут сидеть рядом
4.
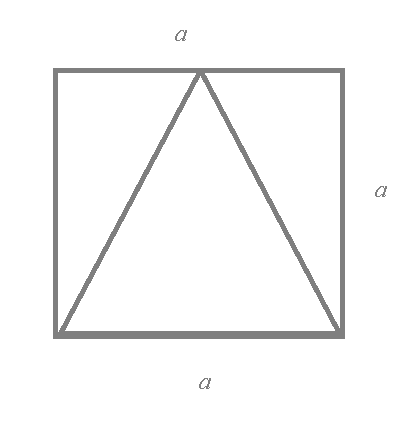
Это геометрическая вероятность
p=S(области)/S_(квадрата).
Пусть сторона квадрата а, тогда высота равнобедренного треугольника равна а
S_(квадрата)=a^2
S_(равнобедренного треугольника)=(1/2)*a*a=a^2/2
S(области)=S_(квадрата)-S_(равнобедренного треугольника)=a^2- (a^2/2)=a^2/2
p=S(области)/S_(квадрата)=1/2
5.
p_(1)=0,04 - вероятность того, что увидит в КАТАЛОГЕ ⇒ q_(1)=1-p_(1) =1-0,04=0,96- вероятность того, что НЕ увидит в КАТАЛОГЕ
p_(2)=0,06- вероятность того, что увидит на СТЕНДЕ ⇒ q_(2)=1-p_(2) =1-0,06=0,94- вероятность того, что НЕ увидит на СТЕНДЕ
p=q_(1)*q_(2)=0,96*0,94=....- вероятность того, что НЕ увидит НИ в КАТАЛОГЕ , НИ на СТЕНДЕ
1.
Имеется шесть цифр.
Если на первом месте 0, то это не шестизначное число.
Значит для заполнения первой цифры шестизначного числа есть 5 способов
Для заполнения второго места есть 4 оставшиеся цифры и 0=5 способов
5*5*4*3*2*1=600 способов получения шестизначных чисел
n=600
Кратные пяти те, которые оканчиваются нулем или 5
m=m_(1)+m_(2)
m_(1)=5*4*3*2*1=120 - оканчивается на 0
m_(1)=4*4*3*2*1 =96- оканчивается на 5
m=120+96=216
p=m/n=216/600=36/100=0,36