Задача 60914 Нужно решить пример со скриншота ...
Условие
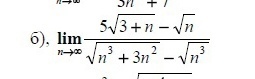
Решение
Неопределенность ( ∞- ∞ ) в числителе и в знаменателе.
Умножаем числитель и знаменатель на [m](5\sqrt{3+n}+\sqrt{n})\cdot(\sqrt{n^3+3n^2}+\sqrt{n^3})[/m]
Применяем формулу: [m](a-b)(a+b)=a^2-b^2[/m]
[m]=\lim_{n \to \infty }\frac{(5\sqrt{3+n}-\sqrt{n})(5\sqrt{3+n}+\sqrt{n})\cdot(\sqrt{n^3+3n^2}+\sqrt{n^3})}{(\sqrt{n^3+3n^2}-\sqrt{n^3})(5\sqrt{3+n}+\sqrt{n})\cdot(\sqrt{n^3+3n^2}+\sqrt{n^3})}=\lim_{n \to \infty }\frac{((5\sqrt{3+n})^2-(\sqrt{n})^2))\cdot(\sqrt{n^3+3n^2}+\sqrt{n^3})}{((\sqrt{n^3+3n^2})^2-(\sqrt{n^3})^2)\cdot 5\sqrt{3+n}+\sqrt{n})}=[/m]
[m]=\lim_{n \to \infty }\frac{((15+5n-n)\cdot(\sqrt{n^3+3n^2}+\sqrt{n^3})}{(n^3+3n^2-n^3)\cdot (5\sqrt{3+n}+\sqrt{n})}=\lim_{n \to \infty }\frac{((15+4n)\cdot(\sqrt{n^3+3n^2}+\sqrt{n^3})}{(3n^2)\cdot (5\sqrt{3+n}+\sqrt{n})}[/m]
Неопределенность ( ∞/∞ )
Делим на [m]n ^{\frac{5}{2}}[/m] и числитель и знаменатель:
[m]\lim_{n \to \infty }\frac{\frac{(15+4n)\cdot(\sqrt{n^3+3n^2}+\sqrt{n^3})}{ n^{\frac{5}{2}}} }{\frac{(3n^2)\cdot (5\sqrt{3+n}+\sqrt{n})}{n^{\frac{5}{2}}} } =\frac{4(1+1)}{3(5+1)}=\frac{8}{18}=\frac{4}{9}[/m]