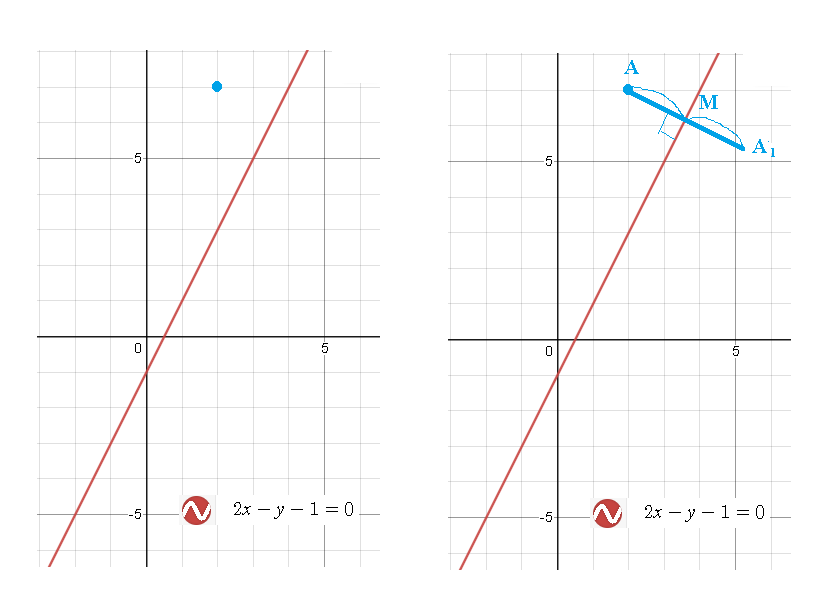
Задача 60285 Найти координаты точки A_1, симметричной...

60d0b90fa1c50e1d3043fa08

21 июня 2021 г. в 19:13

Найти координаты точки A₁, симметричной точке A(2;7) относительно прямой 2x–y–1=0.

exponenta

21 июня 2021 г. в 21:26

★

Составляем уравнение прямой, перпендикулярной данной и проходящей через точку А

Запишем уравнение данной прямой как уравнение с угловым коэффициентом:

y=2x–1

k=2

Произведение угловых коэффициентов взаимо перпендикулярных прямых равно (–1)

Значит угловой коэффициент синей прямой k=–1/2

y=(–1/2)x+b

Чтобы найти b подставляем координаты точки А:

7=(–1/2)·2+b

b=8

y=(–1/2)x+8

Находим точку пересечения двух прямых.

Решаем систему уравнений:
{2x–y–1=0
{y=(–1/2)x+8

2x–((–1/2x)+8)–1=0

x=18/5

x=3,6

y=(–1/2)·3,6+8

y=6,2

M(3,6; 6,2)
M–середина АА₁

(x_A+x_A1)/2=x_M ⇒ x_A1=2x_M–x_A=2·3,6–2=5,2

(y_A+y_A1)/2=y_M ⇒ y_A1=2y_M–y_A=2·6,2–7=5,4

О т в е т. А₁ (5,2; 5,4)