Задача 60246 Найти пределы функции...
Условие
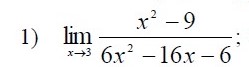
математика ВУЗ
547
Решение
★
Раскладываем на множители
[m]x^2-9=(x-3)(x+3)[/m]
[m]6x^2-16x-6=2(x-3)(3x+1)[/m]
D=(-16)^2-4*6*(-6)=256+144=400
x_(1)=3; x_(2)=-1/3
[m]lim_{x → 3}\frac{x^2-9}{6x^2-16x-6}=lim_{x → 3}\frac{(x-3)(x+3)}{2(x-3)(3x+1)}=lim_{x → 3}\frac{x+3}{2(3x+1)}=\frac{3+3}{2(3\cdot 3 +1)}=...[/m]считайте