Задача 57445 ...
Условие
1. lim (x→x₀) (3x² + 2x - 1) / (2x² + 3x + 1)
a) x₀ = 2
b) x₀ = -1
c) x₀ = ∞
2. lim (x→x₀) (x² + 7x + 12) / (3x² + 11x + 6)
a) x₀ = 2
b) x₀ = -3
c) x₀ = ∞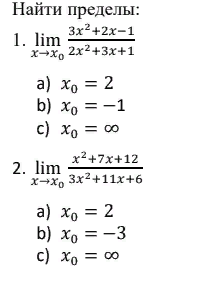
Решение
a)
[m]\lim_{x \to 2 }\frac{3x^2+2x-1}{2x^2+3x+1}=\frac{3\cdot 2^2+2\cdot 2-1}{2\cdot 2^2+3\cdot 2+1}=\frac{12+4-1}{8+6+1}=\frac{15}{15}=1[/m]
б)
[m]\lim_{x \to -1 }\frac{3x^2+2x-1}{2x^2+3x+1}=\frac{3\cdot (-1)^2+2\cdot (-1)-1}{2\cdot (-1)^2+3\cdot (-1)+1}=\frac{3-2-1}{2-3+1}=\frac{0}{0}[/m]
неопределенность.
Раскладываем на множители и числитель и знаменатель:
[m]=\lim_{x \to -1 }\frac{(x+1)(3x-1)}{(x+1)(2x+1)}=[/m]
сокращаем на [m](x+1)[/m]
[m]=\lim_{x \to -1 }\frac{3x-1}{2x+1}=\frac{3\cdot (-1)-1}{2\cdot (-1)+1}=\frac{-3-1}{-2+1}=4[/m]
в)
[m]\lim_{ \to \infty }\frac{3x^2+2x-1}{2x^2+3x+1}=[/m]
Неопределенность ( ∞ / ∞ )
Делим числитель и знаменатель на x^2:
[m]=\lim_{ \to \infty }\frac{\frac{3x^2+2x-1}{x^2}}{\frac{2x^2+3x+1}{x^2}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на [m]x^2[/m] и
каждое слагаемое знаменателя делим на [m]x^2[/m]:
[m]=\lim_{ \to \infty }\frac{\frac{3x^2}{x^2}+\frac{2x}{x^2}-\frac{1}{x^2}}{\frac{2x^2}{x^2}+\frac{3x}{x^2}+\frac{1}{x^2}}=[/m]
[m]=\lim_{ \to \infty }\frac{3+\frac{2}{x}-\frac{1}{x^2}}{2+\frac{3}{x}+\frac{1}{x^2}}=\frac{3+0-0}{2+0+0}=\frac{3}{2}=1.5[/m]