Задача 57424 ...
Условие
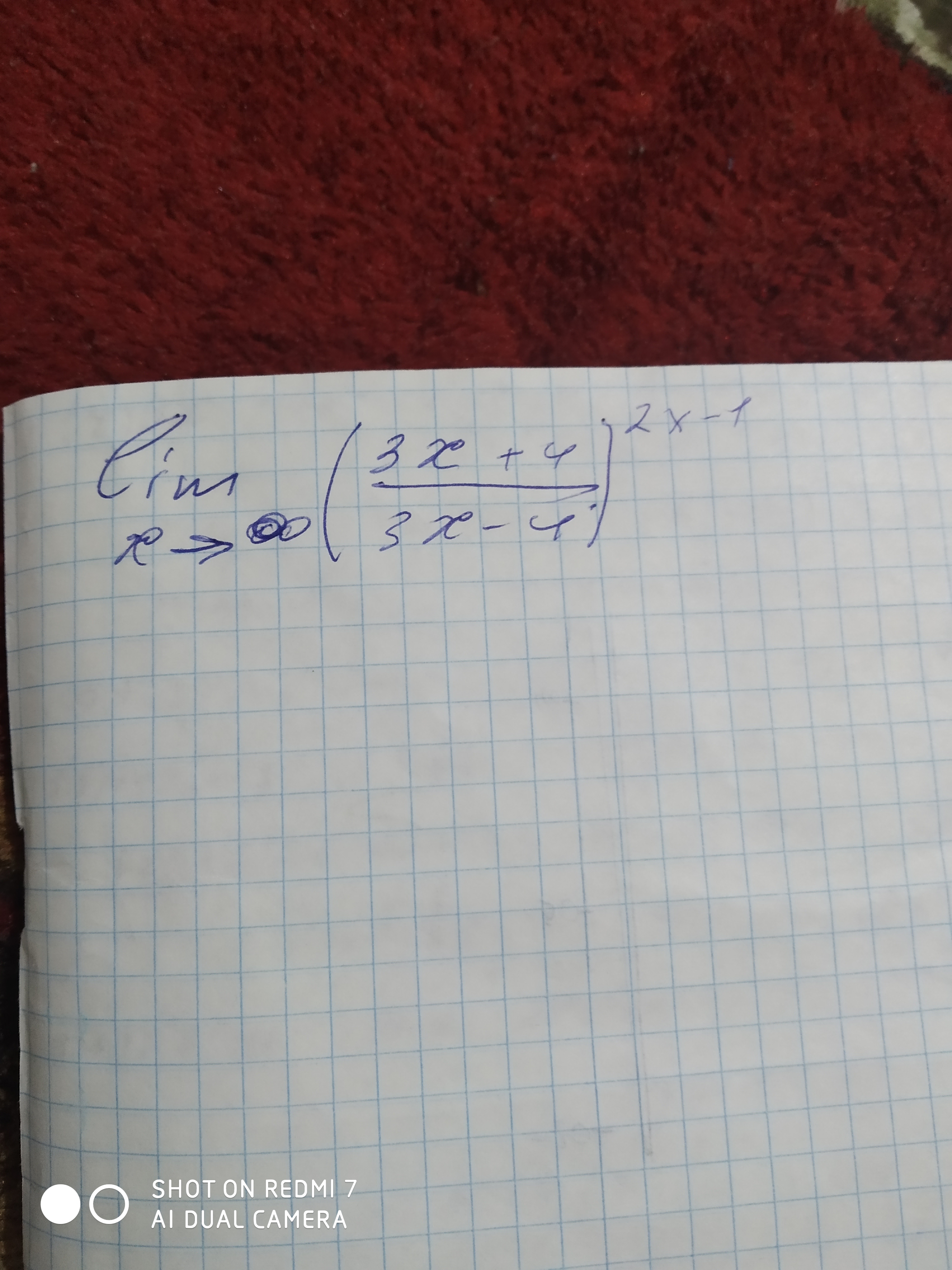
625
Решение
★
[m]\lim_{x \to\infty}(\frac{3x+4}{3x-4})^{2x-1}=\lim_{x \to\infty}(\frac{3x+4}{3x-4})^{2x}\cdot(\frac{3x+4}{3x-4})^{-1} =[/m]
Предел произведения равен произведению пределов.
[m]\lim_{x \to\infty}(\frac{3x+4}{3x-4})^{-1}=1^{-1}=1[/m]
[m]\lim_{x \to\infty}(\frac{3x+4}{3x-4})^{2x}=\lim_{x \to\infty}(\frac{\frac{3x+4}{3x}}{\frac{3x-4}{3x}})^{2x}=[/m]
[m]=\lim_{x \to\infty}\frac{((1+\frac{4}{3x})^{\frac{3x}{4}})^{\frac{8}{3}}}{((1-\frac{4}{3x})^{-\frac{3x}{3}})^{\frac{-8}{3}}}=\frac{e^{\frac{8}{3}}}{e^{\frac{-8}{3}}}=e^{\frac{8}{3}-(-\frac{8}{3})}=e^{\frac{16}{3}}[/m]