Задача 57176 Даны две противоположные вершины...
Условие
другие вершины. Система координат прямоугольная декартова.
Решение
[m]k_{AС}=-\frac{3}{4}[/m]
Тогда
[m]k_{BD}=\frac{4}{3}[/m]
Тогда уравнение BD
[m]y=\frac{4}{3}x+b[/m]
Чтобы найти [m]b[/m] подставим координаты точки [m]О[/m] - середины [m]АС[/m]
[m]О(\frac{-1+6}{2};\frac{4+(-2)}{2})=O(3;1)[/m]
[m]b=-3[/m]
[m]y=\frac{4}{3}x-3[/m]
[m]О[/m] - середина [m]BD[/m]
[m]\frac{x_{B}+x_{D}}{2}=3[/m] ⇒ [blue][m]x_{B}+x_{D}=6[/m] [/blue]
Диагонали квадрата равны.
[m]AC=BD[/m]
[m]AC=\sqrt{(7-(-1))^2+(-2-4)^2}=\sqrt{8^2+6^2}=10[/m]
[m]BD=\sqrt{(x_{D}-x_{B})^2+(y_{D}-y_{B})^2}[/m]
Точки B и D принадлежат прямой [m]y=\frac{4}{3}x-3[/m] ⇒ [m]y_{B}=\frac{4}{3}x_{B}-3[/m] и [m]y_{D}=\frac{4}{3}x_{D}-3[/m]
[m]BD=\sqrt{(x_{D}-x_{B})^2+(y_{D}-y_{B})^2}=\sqrt{(x_{D}-x_{B})^2+(\frac{4}{3}x_{D}-\frac{4}{3}y_{B})^2}=[/m]
[m]=\sqrt{(x_{D}-x_{B})^2+\frac{16}{9}(x_{D}-x_{B})^2}=\sqrt{\frac{25}{9}(x_{D}-x_{B})^2}=\frac{5}{3}|x_{D}-x_{B}|[/m]
[m]\frac{5}{3}|x_{D}-x_{B}|=10[/m]
Из системы:
[m]\left\{\begin {matrix}x_{B}+x_{D}=6\\\frac{5}{3}|x_{D}-x_{B}|=10\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x_{B}+x_{D}=6\\|x_{D}-x_{B}|=6\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x_{B}+x_{D}=6\\x_{D}-x_{B}=6\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}x_{B}+x_{D}=6\\x_{D}-x_{B}=-6\end {matrix}\right.[/m]
[m]x_{D}=6[/m] или [m]x_{D}=0[/m] ⇒
m]x_{B}=0[/m] или [m]x_{D}=6[/m]
Тогда
[m]y_{B}=\frac{4}{3}\cdot 0-3[/m] и [m]y_{D}=\frac{4}{3}\cdot 6-3[/m] ⇒ [m]y_{B}=-3[/m] и [m]y_{D}=5[/m]
[m]y_{B}=\frac{4}{3}\cdot 6-3[/m] и [m]y_{D}=\frac{4}{3}\cdot 0-3[/m]⇒ [m]y_{B}=5[/m] и [m]y_{D}=-3[/m]
О т в е т. [m](0;-3); (6;5)[/m]
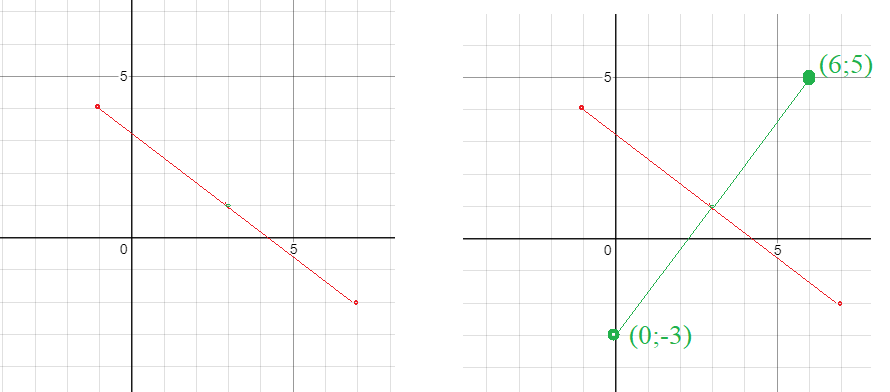
Все решения


