Задача 56745 предел...
Условие
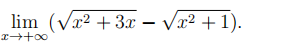
математика колледж
438
Решение
★
Умножаем и делим на [m] (\sqrt{x^2+3x}+\sqrt{x^2+1}) [/m]
[m]lim_{x→ +∞ }\frac{(\sqrt{x^2+3x}-\sqrt{x^2+1})\cdot (\sqrt{x^2+3x}+\sqrt{x^2+1})}{\sqrt{x^2+3x}+\sqrt{x^2+1}}=lim_{x→+ ∞ }\frac{(\sqrt{x^2+3x})^2-(\sqrt{x^2+1})^2}{\sqrt{x^2+3x}+\sqrt{x^2+1}}=[/m]
[m]=lim_{x→+ ∞ }\frac{x^2+3x-x^2-1}{\sqrt{x^2+3x}+\sqrt{x^2+1}}=lim_{x→+ ∞ }\frac{3x-1}{\sqrt{x^2+3x}+\sqrt{x^2+1}}=[/m]
(неопределенность ∞ / ∞)
Делим на х и числитель и знаменатель
[m]=lim_{x→+ ∞ }\frac{\frac{3x-1}{x}}{\frac{\sqrt{x^2+3x}+\sqrt{x^2+1}}{x}}=[/m]
=(3/2)