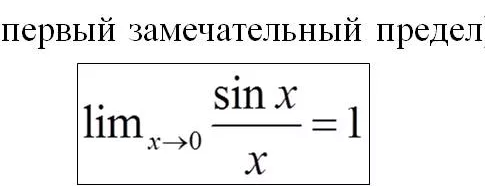Задача 55790 Помогите решить, мы производную не...
Условие
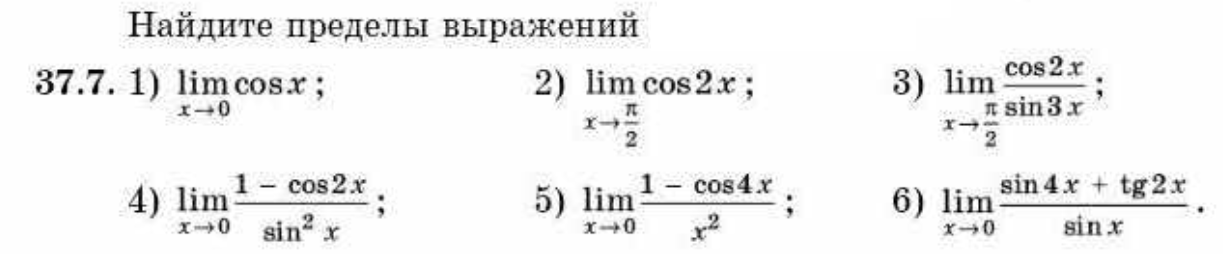
математика 10-11 класс
1036
Решение
★
2)lim_(x →(π/2))cos2x=cos2*(π/2)=cos π=-1;
3)lim_(x →(π/2))[m]\frac{cos2x}{sin3x}=\frac{cosπ}{sin\frac{3π}{2}}=\frac{(-1)}{(-1)}=1[/m]
4)
1-cos2x=2sin^2x
[m]lim_{x →0}\frac{1-cos2x}{sin^2x}=lim_{x →0}\frac{2sin^2x}{sin^2x}=lim_{x →0}2=2[/m]
5)
[m]lim_{x →0}\frac{1-cos4x}{x^2}=lim_{x →0}\frac{2sin^22x}{x^2}=2\cdot lim_{x →0}2\frac{sin2x}{2x}\cdot 2\cdot \frac{sin2x}{2x}=8[/m]
6)
[m]lim_{x →0}\frac{sin4x+tg2x}{sinx}=lim_{x →0}(\frac{sin4x}{sinx}+\frac{tg2x}{sinx})=lim_{x →0}(4\cdot \frac{sin4x}{4x}\cdot \frac{x}{sinx}+2\cdot \frac{tg2x}{2x}\cdot\frac{x}{sinx})=4+2=6[/m]