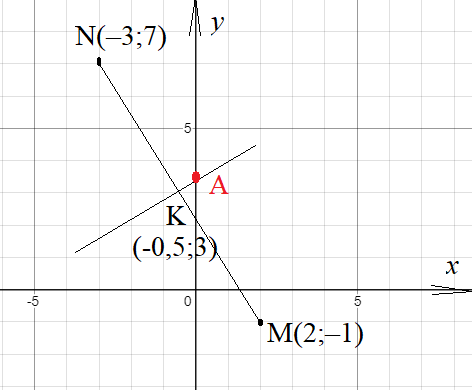
Задача 55739 Знайди координати точки , яка належить...

5fbaa90164081d1dafcb0b61

22 ноября 2020 г. в 21:08

Знайди координати точки , яка належить осі ординат і рівновіддалена від точок М(2;–1),N(–3;7)

exponenta

22 ноября 2020 г. в 21:24

★

Найдем координаты середины отрезка MN

[m] x_{K}=\frac{x_{M}+x_{N}}{2}=\frac{2+(-3)}{2}=-0,5[/m] ⇒
[m] y_{K}=\frac{y_{M}+y_{N}}{2}=\frac{(-1)+7}{2}=3[/m]

Составим уравнение прямой, перпендикулярной MN и проходящей через точку К:

MN: y=kx+b;
Подставляем координаты точки М:
–1=2k+b
Подставляем координаты точки N:
7=–3k+b ⇒ b=3k+7 и подставляем в первое:

–1=2k+3k+7 ⇒ k=5k=–8

k_MN=–1,6

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (–1):
Поэтому угловой коэффициент прямой, перпендикулярной MN
k=5/8
Уравнение прямой, перпендикулярной MN
y=(5/8)x+m

Подставляем координаты точки К:
3=(5/8)·(–0,5)+m

m=51/16

Прямая y=(5/8)x+(51/16) пересекает ось Оу в точке А(0;51/16)

О т в е т. (0;51/16)