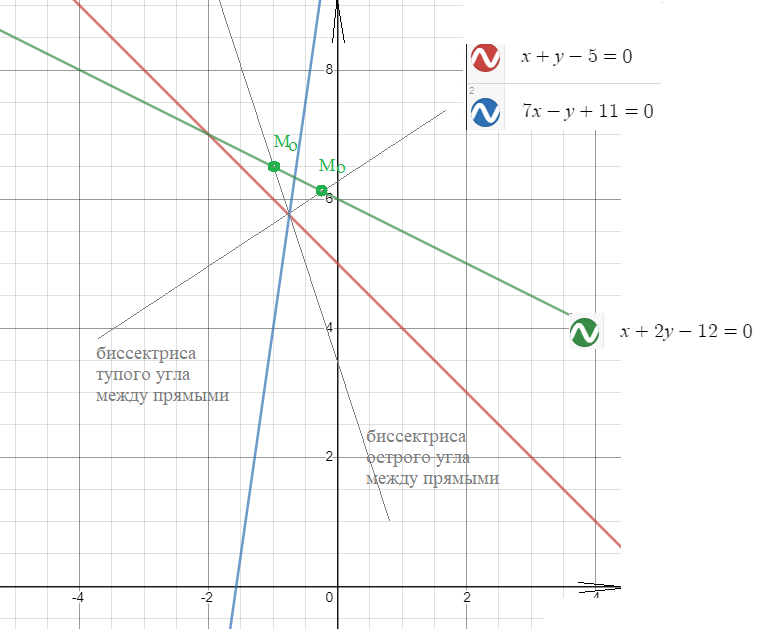
Задача 55486 На прямой x + 2y 12 = 0 найти точки,...

5faab13f322e6f41f4eb5c16

10.11.2020 18:28:17

На прямой x + 2y − 12 = 0 найти точки, равноудаленные от прямых x + y − 5 = 0 и 7x − y + 11 = 0. Сделать рисунок

5f3ea7e3faf909182968ddd9

10.11.2020 20:03:25

★

Пусть M_(o)(x_(o);y_(o)) принадлежит прямой x + 2y − 12 = 0

x_(o) + 2y_(o) − 12 = 0 ⇒ x_(o)=12-2y_(o)

M_(o)(12-2y_(o);y_(o))

Найдем расстояния от точки M_(o) до каждой из прямых:

[m]d_{1}=\frac{|12-2y_{o}+y_{o}-5|}{\sqrt{1^2+1^2}};[/m]

[m]d_{2}=\frac{|7\cdot (12-2y_{o})-y_{o}+11|}{\sqrt{7^2+(-1)^2}}.[/m]



Уравнение: d_(1)=d_(2)
[m]\frac{|12-2y_{o}+y_{o}-5|}{\sqrt{2}}=\frac{|7\cdot (12-2y_{o})-y_{o}+11|}{\sqrt{50}}[/m]

[m]5|12-2y_{o}+y_{o}-5|=|7\cdot (12-2y_{o})-y_{o}+11|[/m] ⇒

[m]5\cdot (12-2y_{o}+y_{o}-5)=7\cdot (12-2y_{o})-y_{o}+11[/m] или [m]5\cdot (12-2y_{o}+y_{o}-5)=-(7\cdot (12-2y_{o})-y_{o}+11)[/m]

Решаем два уравнения и находим координаты двух точек.