Задача 55446 Найти производные a) y = (6x^2 - 2/x^4...

5fa39f25ff76d766b7a0914d

9 ноября 2020 г. в 12:52

Найти производные

a) y = (6x² – 2/x⁴ + 5)²

5f3ea7e3faf909182968ddd9

9 ноября 2020 г. в 13:40

★

Сложная функция вида:

[m]y=u^2[/m]; [m]u=(6x^2-\frac{2}{x^4}+5)[/m]

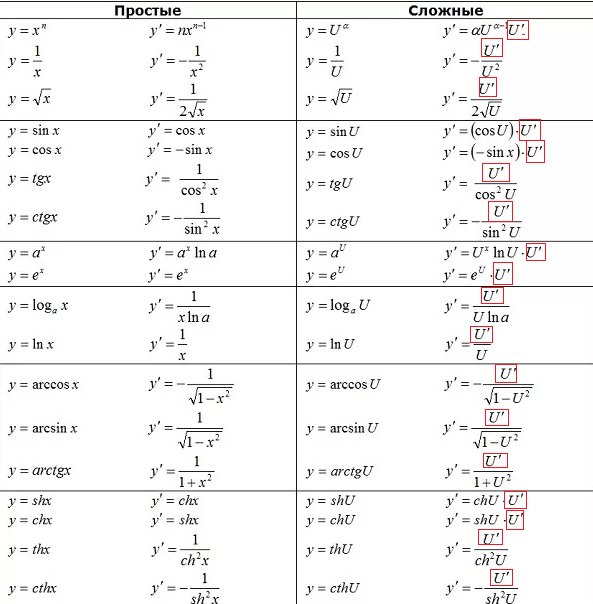
Поэтому по правилу вычисления производной сложной функции ( в таблице производных второй столбик):

[m]y`=2u\cdot u`[/m]


[m]y`=2\cdot (6x^2-\frac{2}{x^4}+5)\cdot (6x^2-\frac{2}{x^4}+5)`=[/m]

[m]=2\cdot (6x^2-\frac{2}{x^4}+5)\cdot ((6x^2)`-(\frac{2}{x^4})`+(5)`)=2\cdot (6x^2-\frac{2}{x^4}+5)\cdot (6\cdot (x^2)`-2\cdot (x^{-4})`+(5)`)=[/m]

[m]=2\cdot (6x^2-\frac{2}{x^4}+5)\cdot (12x-2\cdot (-4)\cdot x^{-4-1}+0)=[/m]


[m]=2\cdot (6x^2-\frac{2}{x^4}+5)\cdot (12x+8\cdot \frac{1}{x^5})[/m] – о т в е т