Задача 55430 помогите с 3 задачей...
Условие
Решение
Составляем уравнение стороны АВ как прямой, проходящей через две точки:
[m]\frac{x+4}{4+4}=\frac{y+5}{1+5}[/m] ⇒ [m]6x-8y-16=0[/m] - нормальный вектор vector{n_(AB)}=(6;-8)-
Этот вектор одновременно является направляющим вектором высоты СН:
vector{s_(CH)}=(6;-8)
Уравнение высоты СН:
[m]\frac{x+0,5}{6}=\frac{y-7}{-8}[/m] ⇒ [m]8x+6y-38=0[/m]
направляющий вектор vector{s_(CH)}=(6;-8)
2.
M(1,75;4) - середина BC
Уравнение медианы АМ как прямой, проходящей через две точки:
[m]\frac{x+4}{1,75+4}=\frac{y+5}{4+5}[/m] ⇒ [m]9\cdot (x+4)=5,75\cdot (y+5)[/m]
направляющий вектор vector{s_(AM)}=(5,75;9)
3.
Угол между прямыми СН и АМ = углу между их направляющими векторами
vector{s_(CH)}=(6;-8)
vector{s_(AM)}=(5,75;9)
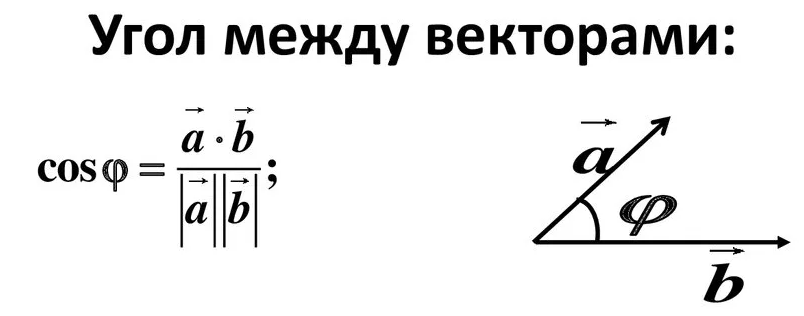
4. угол между векторами:
по формуле:
