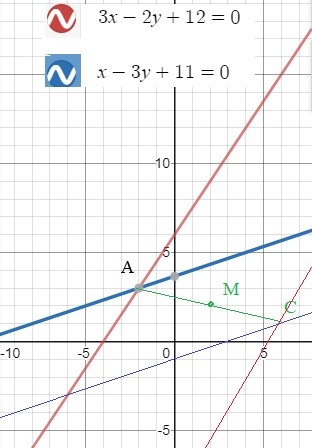
Задача 55307 13. Даны уравнения двух сторон...

5f9fe0ca930cfb5b34aab5d5

04.11.2020 15:51:00

13. Даны уравнения двух сторон параллелограмма [m]3x - 2y + 12 = 0[/m] и [m]x - 3y + 11 = 0[/m], а также точка [m](2;2)[/m] пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма и его диагоналей.
Ответ: [m]3x - 2y - 16 = 0[/m], [m]x - 3y - 3 = 0[/m], [m]x + 4y - 10 = 0[/m], [m]5x - 8y + 6 = 0[/m].

5f3ea7e3faf909182968ddd9

04.11.2020 18:40:53

★

Найдем точку пересечения двух сторон, заданных уравнениями:

[m]\left\{\begin{matrix}3x-2y+12=0\\x-3y+11=0 \end{matrix}\right.[/m]; [m]\left\{\begin{matrix}3\cdot (3y-11)-2y+12=0\\x=3y-11 \end{matrix}\right.[/m] ; [m]\left\{\begin{matrix}y=3\\x=-2\end{matrix}\right.[/m]

Пусть это точка А (-2;3), тогда

точка М ( 2;2) - середина диагонали АС и

[m] x_{M}=\frac{x_{A}+x_{C}}{2}[/m] ⇒ [m] x_{C}=2x_{M}- x_{A}=2\cdot 2-(-2)=6[/m]

[m] y_{M}=\frac{y_{A}+y_{C}}{2}[/m] ⇒ [m] y_{C}=2y_{M}- y_{A}=2\cdot 2-3=1[/m]

Составляем уравнения прямых, параллельным двум данным и проходящим через точку С

[m]3x-2y+12=0[/m] ⇒Уравнение параллельных прямых : [m]3x-2y+m=0[/m]

Подставляем координаты точки С:

[m]3\cdot 6-2\cdot 1+m=0[/m]

[m]m=16[/m]

[m]3x-2y+16=0[/m]- уравнение прямой, параллельной [m]3x-2y+12=0[/m] и проходящей через точку С

Аналогично

[m]x-3y+11=0[/m] ⇒Уравнение параллельных прямых : [m]x-3y+n=0[/m]

Подставляем координаты точки С:

[m]6-3\cdot 1+n=0[/m]

[m]n=-3[m]

[m]x-3y-3=0[/m] - уравнение прямой, параллельной [m]x-3y+11=0[/m] и проходящей через точку С


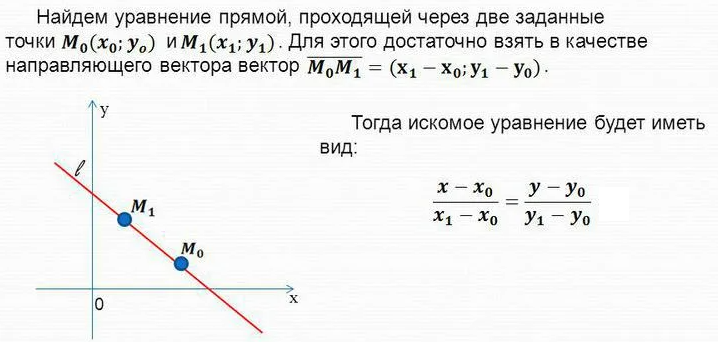
Уравнение диагонали АС как прямой, проходящей через две точки: A и M ( или А и С, см формулу в скрине)

Найдем координаты точки B - точки пересечения [m]x-3y+11=0[/m] и [m]3x-2y+16=0[/m]

[m]\left\{\begin{matrix}
x-3y+11=0\\3x-2y+16=0 \end{matrix}\right.[/m]

Уравнение диагонали BD как прямой, проходящей через две точки: B и M ( см формулу в скрине)