Задача 55290 срочно продифференцировать данные...
Условие
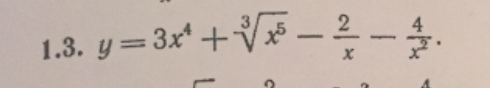
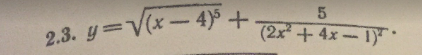
Решение
[m]=3\cdot 4x^3+\frac{5}{3}\cdot x^{\frac{5}{3}-1}-2\cdot (-1)\cdot x^{-1-1}-4\cdot (-2)\cdot x^{-2-1}=12x^3+\frac{5}{3}\cdot x^{\frac{2}{3}}+2\cdot\frac{1}{x^2}+4\cdot\frac{1}{x^3}=[/m]
[m]=12x^3+\frac{5}{3}\cdot \sqrt[3]{x^{2}}+2\cdot\frac{1}{x^2}+4\cdot\frac{1}{x^3}[/m]
[m]y`=(\sqrt{(x-4)^5}+\frac{5}{(2x^2+4x-1)^2})`=(\sqrt{(x-4)^5})`+(\frac{5}{(2x^2+4x-1)^2})`=((x-4)^{\frac{5}{2}})`+5\cdot (2x^2+4x-1)^{-2})`=[/m]
[m]=\frac{5}{2}\cdot (x-4)^{\frac{5}{2}-1}\cdot (x-4)`+5\cdot (-2)\cdot (2x^2+4x-1)^{-2-1}\cdot (2x^2+4x-1)`=[/m]
[m]=\frac{5}{2}\cdot (x-4)^{\frac{3}{2}}-10 (2x^2+4x-1)^{-3}\cdot (4x+4)=\frac{5}{2}\cdot \sqrt{(x-4)^3}-10\cdot \frac{4x+4}{(2x^2+4x-1)^3}=[/m]
[m]=\frac{5}{2}\cdot(x-4)\cdot \sqrt{x-4}-40\cdot \frac{x+1}{(2x^2+4x-1)^3}[/m]