Задача 55245 Вычислить пределы функций, не используя...
Условие
(вариант на фото)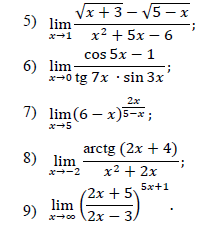
Решение
[m]\lim_{x \to 1}\frac{\sqrt{x+3}-\sqrt{5-x}}{x^2+5x-6}=\frac{\sqrt{1+3}-\sqrt{5-1}}{1+5-6}=\frac{0}{0}[/m]
Неопределенность
Знаменатель раскладываем на множители:
[m]x^2+5x-6=(x-1)(x+6)[/m]
Умножаем и числитель и знаменатель на выражение
[m]\sqrt{x+3}+\sqrt{5-x}[/m]
Получаем:
[m]=\lim_{x \to 1}\frac{(\sqrt{x+3}-\sqrt{5-x})(\sqrt{x+3}+\sqrt{5-x})}{(x-1)(x+6)(\sqrt{x+3}+\sqrt{5-x})}=[/m]
Применяем формулу разности квадратов a^2-b^2=(a-b)*(a+b)
[m]\lim_{x \to 1}\frac{(\sqrt{x+3})^2-(\sqrt{5-x})^2}{(x-1)(x+6)(\sqrt{x+3}+\sqrt{5-x})}=\lim_{x \to 1}\frac {x+3-(5-x)}{(x-1)(x+6)(\sqrt{x+3}+\sqrt{5-x})}=[/m]
[m]=\lim_{x \to 1}\frac {x+3-5+x}{(x-1)(x+6)(\sqrt{x+3}+\sqrt{5-x})}=\lim_{x \to 1}\frac {2(x-1)}{(x-1)(x+6)(\sqrt{x+3}+\sqrt{5-x})}[/m]
Сокращаем (на x-1)
[m]=\lim_{x \to 1}\frac {2}{(x+6)(\sqrt{x+3}+\sqrt{5-x})}=\frac{2}{(1+6)\cdot( \sqrt{4}+\sqrt{4})}=\frac{1}{14}[/m]
6.
[m]\lim_{x \to 0}\frac{cos5x-1}{tg7x\cdot sin3x}=\frac{cos0-1}{0\cdot 0}=\frac{0}{0}[/m]
Неопределенность
По формуле: [m] cos2 α =cos^2 α -sin^2 α [/m] ⇒ [m] cos2 α =(1-sin^2 α) -sin^2 α=1-2sin^2 α [/m]
получим:
[m] cos5x-1=-2sin^2\frac{5x}{2}[/m]
[m]=\lim_{x \to 0}\frac{(-2sin^2\frac{5x}{2})}{tg7x\cdot sin3x}=-2\cdot \lim_{x \to 0}\frac{sin\frac{5x}{2}\cdot sin\frac{5x}{2}}{tg7x\cdot sin3x}=-2\cdot \lim_{x \to 0}\frac{sin\frac{5x}{2}}{\frac{5x}{2}}\cdot \frac{sin\frac{5x}{2}}{\frac{5x}{2}}\cdot \frac{7x}{tg7x}\cdot \frac{3x}{sin3x}\cdot \frac{\frac{5x}{2}\cdot \frac{5x}{2}}{7x\cdot 3x}=[/m]
[m]=-2\cdot 1\cdot 1\cdot 1\cdot 1\cdot\frac{\frac{5}{2}\cdot \frac{5}{2}}{7\cdot 3}=-\frac{25}{42} [/m]