Задача 55151 найти производную функции y,заданной...
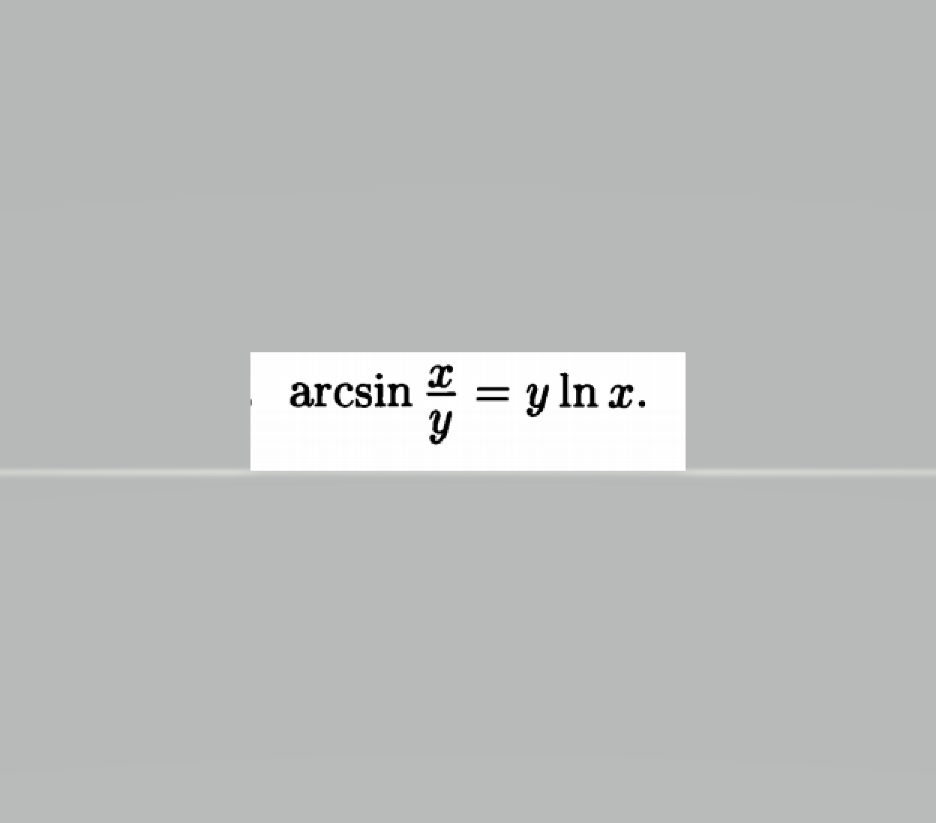
Условие
Решение
(arcsin(x/y))`=(y*lnx)
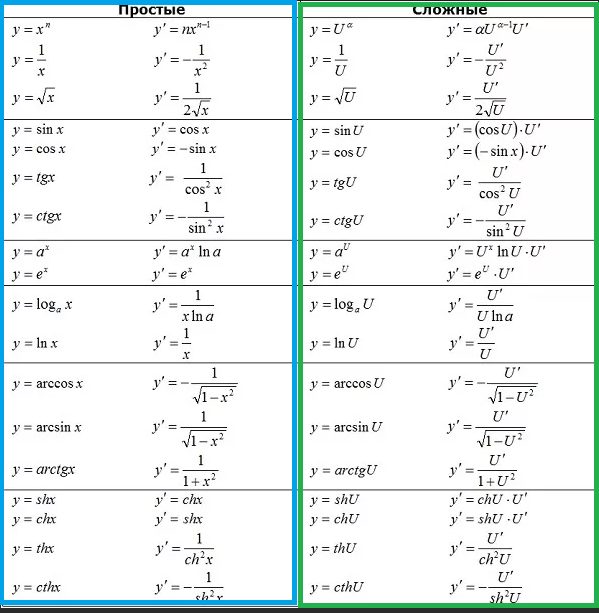
при этом х - независимая переменная, формулы для производной в первом столбике таблицы производных,
у - зависимая, сложная функция, формулы во втором столбике.
[m] (lnx)`=\frac{1}{x}[/m], а если бы было в решении [m] (lny)`= \frac{1}{y}\cdot y`[/m]
[m] (arcsin x)`=\frac{1}{\sqrt{1-x^2}}[/m], а если бы было в решении [m] (arcsiny)`= \frac{1}{\sqrt{1-y^2}}\cdot y`[/m]
В данном примере так:
[m]\frac{1}{\sqrt{1-(\frac{x}{y})^2}}\cdot (\frac{x}{y})`=y`\cdot lnx+y\cdot (lnx)`[/m]
[m](\frac{x}{y})`=\frac{x`\cdot y-x\cdot y`}{y^2}[/m]
[m]x`=1[/m] ; [m]y`=y`[/m]
[m]\frac{1}{\sqrt{1-(\frac{x}{y})^2}}\cdot\frac{ y-x\cdot y`}{y^2}=y`\cdot lnx+y\cdot \frac{1}{x}[/m]
Переносим слагаемые с y` в одну сторону
и
находим y` из равенства