Задача 53327 cos2x+sin^2x = 3/4, [Pi;...
Условие
sin(Pi/2+x) = sin2x, [-Pi; Pi/2]
cos2x-5sqrt(2)cosx-5 = 0, [-3Pi; -3Pi/2]
Решение
Простейшие решают по формулам.
1)
cos2x=1-2sin^2x
1-2sin^2x+sin2^x=3/4
sin^2x=1/2
[b]sinx=1/2 [/b] или [b]sinx=-1/2[/b]
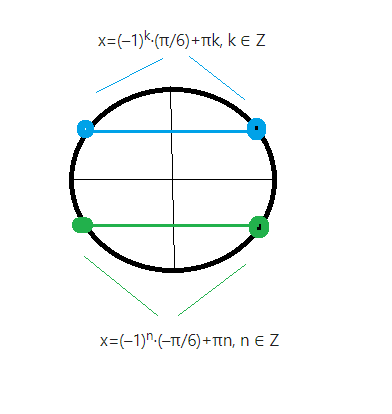
x=(-1)^(k)*(π/6)+πk, k ∈ Z или x=(-1)^(n)*(-π/6)+πn, n ∈ Z
Cм. рис. 1
Корни x=(-1)^(k)*(π/6)+πk, k ∈ Z в 1 и 2 четверти
x=(-1)^(n)*(-π/6)+πn, n ∈ Z в 3 и 4 четвертях
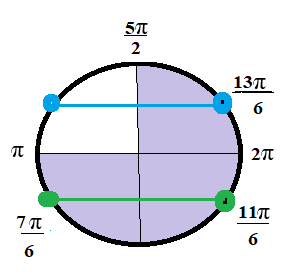
Отбор корней на отрезке:
см. рис. 2
О т в е т. 7π/6; 11π/6; 13π/6
2)
По формулам приведения: sin((π/2)+x)=cosx
Уравнение принимает вид:
cosx =sin2x
cosx=2sinx*cosx
2sinx*cosx-cosx=0
cosx*(2sinx-1)=0
[b]cosx=0 [/b] или [b] 2sinx-1=0[/b] ⇒ [b]sinx=1/2[/b]
[b]cosx=0 [/b] ⇒ x=(π/2)+πk, k ∈ Z
[b]sinx=1/2[/b] ⇒ x=(-1)^(k)*(π/6)+πk, k ∈ Z
Отрезку [-π;π/2] принадлежат корни:
-π/6; π/2
3)
cos2x=2cos^2x-1
2cos^2x-5sqrt(2)cosx-6=0
D=50-4*2*(-6)=98
sqrt(D)=7sqrt(2)
[b]сosx=-sqrt(2)/2; [/b] cosx=3sqrt(2) - уравнение не имеет корней, |cosx| ≤ 1, 3sqrt(2)>1
[b]сosx=-sqrt(2)/2; [/b]⇒ x= ± (3π/4)+2πn, n ∈ Z
Отрезку [-3π;-3π/2] принадлежат корни:
- (3π/4)-2π=-11π/4;- (3π/4)
(3π/4)-2π=-5π/4