Задача 46811 Помогите,пожалуйста,решить...
Условие
А затем найти вторую производную.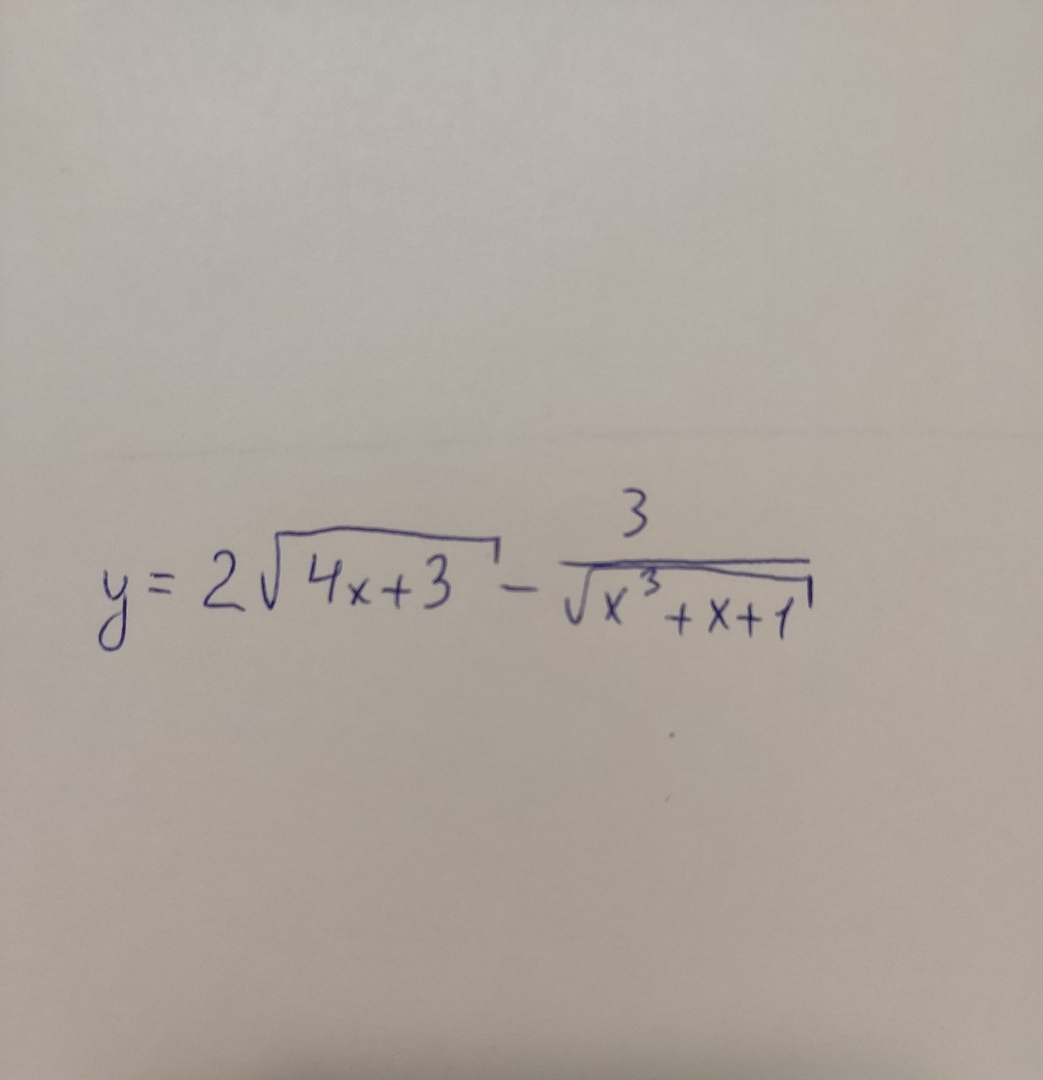
математика ВУЗ
682
Все решения
y`=2*(1/2)*(4x+3)^(-1/2)*(4x+3)` - 3*(-1/2)*(x^3+x+1)^(-3/2)*(x^3+x+1)`;
y`=4*(4x+3)^(-1/2)+(3/2)*(3x^2+1)*(x^3+x+1)^(-3/2)
y``=4*(-1/2)*(4x+3)^(-3/2)*4 +(3/2)*(3x^2+1)`*(x^3+x+1)^(-3/2)+(3/2)*(3x^2+1)*(-3/2)*(x^3+x+1)^(-5/2)*(x^3+x+1)`
y``=-8*(4x+3)^(-3/2)+9x^2*(x^3+x+1)^(-3/2)+(9/4)(3x^2+1)^2*(x^3+x+1)^(-5/2)