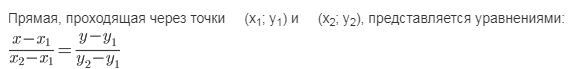Задача 46800 Найти расстояние до точки А(3;7),...

kamilova009

2020-04-12 20:16:49

Найти расстояние до точки А(3;7), проходящей через точки В (-2;4), С(5;1)

sova

2020-04-12 20:21:16

Составляем уравнение прямой ВС, как прямой , проходящей через две точки ( см формулу в приложении)

[m]\frac{x-5}{-2-5}=\frac{y-1}{4-1}[/m]

[m]3(x-5)=-7(y-1)[/m]

[b]3x+7y-22=0[/b]

Применяем формулу нахождения расстояния от точки А до прямой
ВС: 3х+7y-22=0

(cм. приложение 2)

d=[m]\frac{3\cdot 3+7\cdot 7 -22}{\sqrt{3^2+7^2}}=\frac{36}{\sqrt{58}}[/m]



[i]Второй способ[/i]

Составляем уравнение прямой ВС в виде y=kx+b

Подставляем координаты точек B и C

4=k*(-2)+b
1=k*5+b

Вычитаем из первого уравнения второе
3=-7k
k=-3/7 ⇒ b=1-5*(-3/7)=22/7

y=([b]-3/7[/b])x+(22/7)

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)

Значит прямая, перпендикулярная ВС имеет угловой коэффициент
(7/3)

Уравнение таких прямых
y=(7/3)x+b

Чтобы найти b подставляем координаты точки А

7=(7/3)*3+b

b=0

y=(7/3)x - уравнение прямой, перпендикулярной ВС и проходящей через точку А

Находим точку пересечения этой прямой с прямой ВС

{y=-(3/7)x+(22/7)
{y=(7/3)x

x=33/43

y=77/43

Это координаты точки Н - основания перпендикуляра АН на сторону ВС

Находим расстояние АН

AH=sqrt((x_(H)-x_(A))^2+(y_(H)-y_(A))^2)=

считаем самостоятельно.
Ответы должны быть одинаковые