Задача 45716 ...
Условие
3) y = (4x^6 - 7x^2 + 9x + π/4)^4
4) y = (9x - 1)^5 + √(5 - x^2)
5) y = ((5 - 2x)^3) / (3x + 7)^4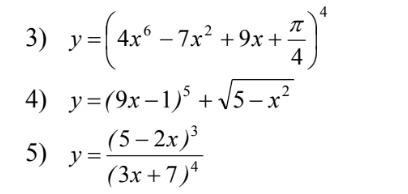
Решение
[m]y`=4\cdot (4x^6-7x^2+9x+\frac{\pi}{4})\cdot (4x^6-7x^2+9x+\frac{\pi}{4})`[/m]
[m]y`=4\cdot (4x^6-7x^2+9x+\frac{\pi}{4})\cdot (24x^5-14x+9+0)[/m]
[m]y`=4\cdot (24x^5-14x+9)\cdot (4x^6-7x^2+9x+\frac{\pi}{4})[/m]
4.
[m]y`=5\cdot(9x-1)^{4}\cdot(9x-1)`+\frac{(5-x^2)`}{2\sqrt{5-x^2}}[/m]
[m]y`=5\cdot(9x-1)^{4}\cdot 9+\frac{(-2x)}{2\sqrt{5-x^2}}[/m]
[m]y`=45 \cdot (9x-1)^{4}-\frac{x}{\sqrt{5-x^2}}[/m]
5.
Логарифмируем:
[m]lny=ln(5-2x)^{3}-ln(3x+7)^{4}[/m]
[m]lny=3ln(5-2x)-4ln(3x+7)[/m]
Дифференцируем обе части:
[m]\frac{y`}{y}=3\frac{(5-2x)`}{5-2x}-4\frac{(3x+7)`}{3x+7}[/m]
[m]\frac{y`}{y}=3\frac{(-2)}{5-2x}-4\frac{3}{3x+7}[/m]
[m]\frac{y`}{y}=-\frac{6}{5-2x}-\frac{12}{3x+7}[/m]
[m]\frac{y`}{y}=-6(\frac{(3x+7)+2\cdot (5-2x)}{(5-2x)(3x+7)})[/m]
[m]\frac{y`}{y}=-6(\frac{3x+7+10-4x}{(5-2x)(3x+7)})[/m]
[m]y`=-6\cdot y \cdot (\frac{17-x}{(5-2x)(3x+7)})[/m]
[m]y`=-6\frac{(5-2x)^{3}}{(3x+7)^{4}}\cdot (\frac{17-x}{(5-2x)(3x+7)})[/m]
[m]y`=-6\frac{(5-2x)^{2}\cdot (17-x)}{(3x+7)^{5}}[/m]