Задача 45324 ...
Условие
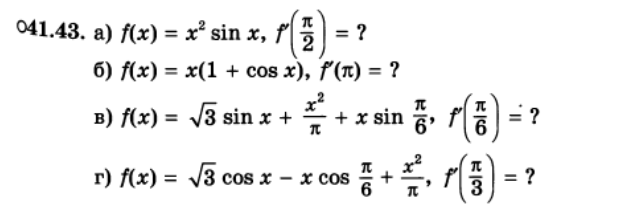
Решение
f `(π/2)=2*(π/2)*sin(π/2)+(π/2)^2*cos(π/2)=
так как sin(π/2)=1; cos(π/2)=0
=2*(π/2)*1+0=[b]π[/b]
б)
f `(x)=(x)`*(1+cosx)+x*(1+cosx)`=(1+cosx)+x*(-sinx)=1+cosx-x*sinx
f `(π)=1+cosπ-π*sinπ=
так как sinπ=0; cosπ=-1
=1+(-1)-π*0=[b]0[/b]
в)
[m]f `(x)=\sqrt{3}\cdot cosx+\frac{2x}{\pi}+sin\frac{\pi}{6}[/m]
[m]f `(\frac{\pi}{6})=\sqrt{3}\cdot cos\frac{\pi}{6}+\frac{2\cdot \frac{\pi}{6}}{\pi}+sin\frac{\pi}{6}=\sqrt{3}\cdot \frac{\sqrt{3}}{2}+\frac{1}{3}+\frac{1}{2}=\frac{7}{3}[/m]
г)
[m]f `(x)=\sqrt{3}\cdot (-sinx)-cos\frac{\pi}{6}+\frac{2x}{\pi}[/m]
[m]f `(\frac{\pi}{3})=-\sqrt{3}\cdot sin\frac{\pi}{3}-cos\frac{\pi}{6}+\frac{2\cdot \frac{\pi}{3}}{\pi}=-\sqrt{3}\cdot \frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}+\frac{2}{3}=[/m]
