Задача 45250 Найти производную dy/dx функции,...
Условие
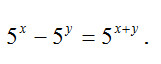
математика ВУЗ
839
Решение
★
х- независимая переменная, поэтому x`=1
y-зависимая переменная, функция поэтому y` есть y`
ее-то и ищем
5^(x)*ln5 - 5^(y)*y`*ln5=5^(x+y)*(x+y)`*ln5
5^(x)*ln5 - 5^(y)*y`*ln5=5^(x+y)*(1+y`)*ln5
5^(x)*ln5 - 5^(y)*y`*ln5=5^(x+y)*ln5+5^(x+y)*y`*ln5
Делим на ln5
Переносим слагаемые с y` вправо:
5^(x) - 5^(x+y)=(5^(x+y)+5^(y))*y`
[m]y`=\frac{5^{x}-5^{x+y}}{5^{x+y}+5^{y}}[/m]