Задача 42582 4 задание пределы с помощью По второму...
Условие
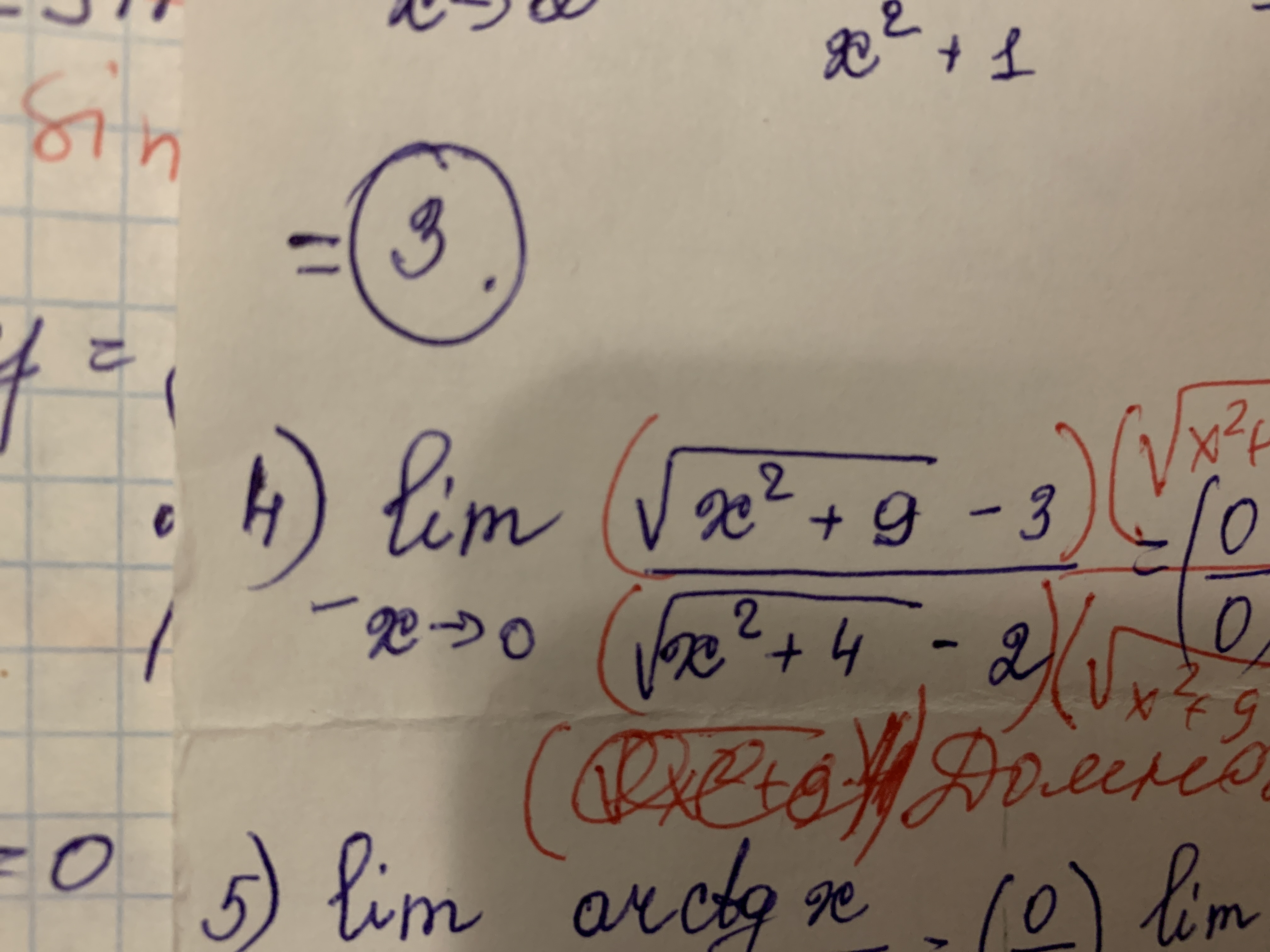
Все решения
Умножаем и числитель и знаменатель на
(sqrt{x^{2}+9}+3)*(sqrt{x^{2}+4}+2)
[m]=\lim_{x \to 0}\frac{(\sqrt{x^{2}+9}-3)(\sqrt{x^{2}+9}+3)(\sqrt{x^{2}+4}+2)}{(\sqrt{x^{2}+4}-2)(\sqrt{x^{2}+9}+3)(\sqrt{x^{2}+4}+2)}=[/m]
Применяем формулу разности квадратов a^2-b^2=(a-b)*(a+b)
[m]\lim_{x \to 0}\frac{((\sqrt{x^{2}+9})^2-3^2)(\sqrt{x^{2}+4}+2)}{(()\sqrt{x^{2}+4})^2-2^2)(\sqrt{x^{2}+9}+3)}=\lim_{x \to 0}\frac{x^{2}(\sqrt{x^{2}+4}+2)}{x^{2}(\sqrt{x^{2}+9}+3)}=[/m]
Сокращаем на x^2
[m]=\lim_{x \to 0}\frac{\sqrt{x^{2}+4}+2}{\sqrt{x^{2}+9}+3}=\frac{\sqrt{4}+2}{\sqrt{9}+3}=\frac{4}{6}=\frac{2}{3}[/m]