Задача 36640 1)найти площадь фигуры ограниченной...

katya1837

2019-05-01 13:18:56

1)найти площадь фигуры ограниченной линиями: y=x^3,y=8,x=0
2) найти объём тела полученного вращением вокруг оси ox фигуры , ограниченной линиями : x^2+y=0,x=1,y=0

sova

2019-05-01 13:32:14

1.
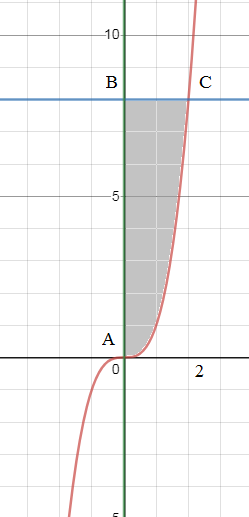
Находим координаты точек пересечения графиков
y=x^3 и у =8

x^3=8
x=2

См. область на рисунке.

S= ∫ ^(2)_(0)(8-x^3)dx=(8x-(x^4/4))|^(2)_(0)=8*2-(2^4/4)=16-4=12

2.
V_(Ox)=π ∫ ^(b)_(a)f^2(x)dx=π ∫^(1)_(0)(-x^2)^2dx=[y=-x^2;f(x)=-x^2]

= π∫^(1)_(0)x^4dx=π*(x^5/5)|^(1)_(0)= [b](1/5)π[/b]