Задача 35284 Без использования метода с частными...
Условие
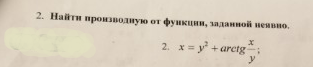
математика ВУЗ
993
Решение
★
x- независимая переменная
x`=1
y=y(x) - функция
1=2y*y`+(1/(1+(x/y)^2) )*(x/y)`
1=2y*y`+(y^2/(x^2+y^2))*(x`*y-x*y`)/y^2
1=2y*y`+(y-xy`/(x^2+y^2))
1=2y*y`+(y/(x^2+y^2)) - (xy`)/(x^2+y^2)
Переносим слагаемые с у` влево
(xy`)/(x^2+y^2) - 2y*y`=(y/(x^2+y^2)) - 1
y`*( x/(x^2+y^2) -2y) = (y-x^2-y^2)/x^2+y^2)
y`= [b](y-x^2-y^2)/(x-2x^2y-2y^3)[/b]
Все решения
1=2yy'+(y-y'x)/(x^2+y^2)
Еще пример можно посмотреть здесь https://youtu.be/RKGRT3nr2Tc
