Задача 34856 Вычислить пределы функций, не пользуясь...
Условие
исчисления.
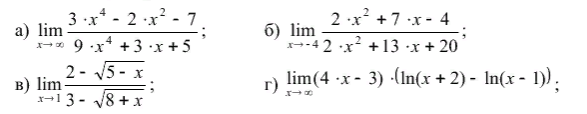
Решение
Делим и числитель и знаменатель на x^4:
lim_(x→∞)(3-(2/x^2)-(7/x^4))/(9+(3/x^3)+(5/x^4))=(3+0+0)/(9+0+0)=1/3
При x→∞
2/x^2
7/x^4
3/x^3
5/x^4
бесконечно малые функции, их предел равен 0
2)Неопределенность (0/0)
Раскладываем числитель и знаменатель на множители и сокращаем на (х+4)
lim_(x→(-4))(х+4)*(2x-1)/(x+4)*(2x+5)=
=lim_(x→(-4))(2x-1)/(2x+5)=(-8-1)/(-8+5)=3
3)Неопределенность (0/0)
Умножаем и числитель и знаменатель на
(2+sqrt(5-x))*(3+sqrt(8+x))
Применяем формулу
(sqrt(a)-sqrt(b))*(sqrt(a)+sqrt(b))=a-b
lim_(x→1) (4-(5-х))*(3+sqrt(8+x))/(9-(8+x))*(2+sqrt(5-x))=
= lim_(x→1) (х-1)*(3+sqrt(8+x))/(1-x)*(2+sqrt(5-x))=
сокращаем на (х-1)
= - lim_(x→1) (3+sqrt(8+x))/(2+sqrt(5-x))=-(3+3)/(2+2)=-3/2
4)
f(x)=(4x-3)*(ln(x+2)-ln(x-1))
Разность логарифмов заменим логарифмом частного
f(x)= (4x-3)*ln ((x+2)/(x-1))
Применяем свойства логарифма степени
f(x)=ln((x+2)/(x-1))^(4x-3)
f(x)=ln((x+2)/(x-1))^(4x)* ((x+2)/(x-1))^(-3)
Логарифм произведения равен сумме логарифмом
ln((x+2)/(x-1))^(4x)+ ln ((x+2)/(x-1))^(-3)
lim_(x→∞) [b]([/b] ln((x+2)/(x-1))^(4x) + ln ((x+2)/(x-1))^(-3) [b] ) [/b]
предел суммы равен сумме пределов
Считаем предел первого слагаемого
lim_(x→∞) ln((x+2)/(x-1))^(4x)= ln lim_(x→∞) ((x+2)/(x-1))^(4x)
знак предела и знак непрерывной функции можно менять местами
имеем неопределенность 1^( ∞)
Применяем второй замечательный предел.
Делим и числитель и знаменатель дроби на x
ln lim_(x→∞) ((1+(2/x))/(1-(1/x)))^(4x)=
=ln lim_(x→∞) (1+(2/x))^(4x)/(1-(1/x))^(4x)=
=ln (e^2)/e^(-4)=lne^(6)=6
Считаем предел второго слагаемого
lim_(x→∞) ln((x+2)/(x-1))^(-3)= ln lim_(x→∞) ((x+2)/(x-1))^(-3)
знак предела и знак непрерывной функции можно менять местами
= ln (1^(-3))=ln1=0
О т в е т. 6+0=6