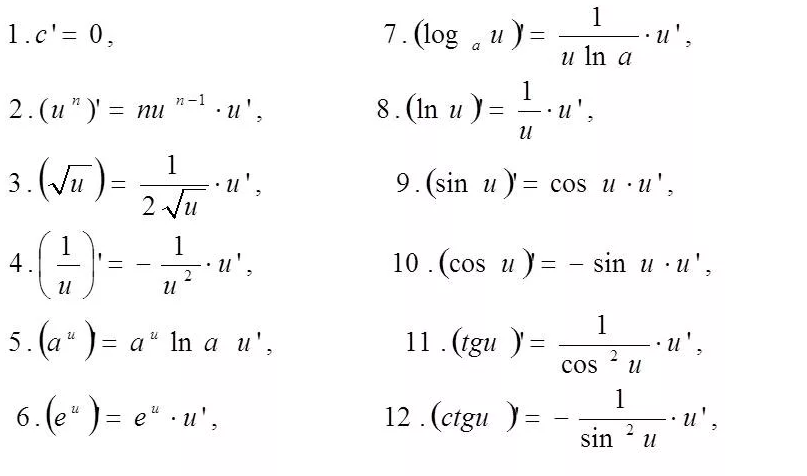Задача 33478 Задание на картинке...

marinabulka

2019-02-11 20:50:21

Задание на картинке

sova

2019-02-11 21:26:42

★

1.
y`=(5x^7-2x^3-∛x+3x^(-2)+15)`=
производная суммы ( разности) равны сумме ( разности) производных;
константу можно выносить за знак производной
(С)`=0
[b](x^( α ))`= α *x^( α -1)[/b]

=5*7x^(6) -2*3*x^2 -(1/3)x^(-2/3)+3*(-2)*x^(-3)+0=
=35x^6-6x^2-1/(3∛(x^2))-6/(x^3);
2
[b](x^( α ))`= α *x^( α -1)[/b]
y`=2*(x^(-2)/(-2))-3*(x^(-3)/(-3))+4*(x^(-4)/(-4))-(6/5)*(x^(-5)/(-5))=

=(-1/x)+(1/x^3)-(1/x^4)+(6/25)*(1/x^5)

3.
a^(m)*a^(n)=a^(m+n)
[b](x^( α ))`= α *x^( α -1)[/b]

y=3*x^(1/4)=10x^(11/3)-5x^(13/5)-4x^(-3)
y`=3*(1/4)*x^(-3/4)+10*(11/3)x^(8/3)-5*(13/5)x^(8/5)-4*(-3)x^(-4)
y`=(3/4)*(1/∛(x^4))+(110/3)x^2∛(x^2) -13x*(x^(3/5))+12/(x^4)

4. y=u*v
y`=u`*v+u*v`
y`=(5cosx-3tgx)`*sinx+(5cosx-3tgx)*(sinx)`=
=(5*(-sinx)-3*(1/cos^2x))*sinx+(5cosx-3tgx)*cosx

5.
y=(u/v)
y`=(u`*v-u*v`)/v^2

y`=(6ctgx)`*(sinx-2x)-6ctgx*(sinx-2x)`)/(sinx-2x)^2

y`=(-6/sin^2x)*(sinx-2x) - 6ctgx*(cosx-2))/(sinx-2x)^2

6.
y=cosu, u=5х+3
y`=(cosu)`*u`

y`=3*(-sin(5x+3))*(5x+3)`
y`=-15sin(5x+3)

7.
y=u^3
u=kn(arctgx-2x^3)

y`=3u^2*u`

y`=3ln^(2)(arctgx-2x^3) * (arctgx-2x^3)`;
y`=3ln^2(arctgx-2x^3) * (1/(1+x^2) - 6x^2)

8.
y`=(1/3)*(cos2x)*(2x)`+ (1/3)*(1/ctg2x)*(ctg2x)`

y`=(2/3)cos2x + (2/3)*(1/ctg2x)*(-1/sin^22x)

9.
y=log_(2)(1-tg6x) - log_(2)(1+tg6x)

(log_(2)u)`=(1/u)*(u`)*(1/ln2) - cм. формула 7

y`=(1/ln2)*(1/(1-tg6x))*(1-tg6x)`- (1/ln2)*(1/(1+tg6x))*(1+tg6x)`

y`=(1/ln2)*(1/(1-tg6x))*(-1/cos^26x)*(6x)` - (1/ln2)*(1/(1+tg6x))*(1/cos^2x)*(6x)`
(6x)`=6

y`=(6/ln2)*(1/cos^2x) * [b]((-1-tg6x-1+tg6x)/(1-tg^26x))[/b]=

=(6/ln2)*(1/cos^2x) * [b]((-2)/(1-tg^26x))[/b]