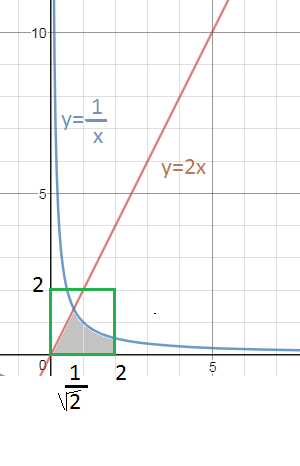Задача 29187 Нужны решения: 1....

slava191

02.08.2018

Нужны решения:

1. [link=https://reshimvse.com/zadacha.php?id=23978]
2. [link=https://reshimvse.com/zadacha.php?id=23979]
3. [link=https://reshimvse.com/zadacha.php?id=23975]

SOVA

03.08.2018

★

1.
23978
{0 меньше или равно x меньше или равно 2
{0 меньше или равно y меньше или равно 2
{xy меньше или равно 1;
{y/x меньше или равно 2

См. рис. 1

Первые два неравенства задают квадрат [0;2]×[0;2]

По формуле геометрической вероятности

p=S(области)/S(квадрата)

S(квадрата)=2*2=4

Найдем абсциссы точки пересечения
прямой y=2x и гиперболы y=1/x
2x=1/x
2x^2=1
x=±sqrt(1/2)

S(области)=∫ ∫_(D) dxdy=

= ∫^(sqrt(1/2)) _(0)dx ∫^(2x)_(0)dy + ∫^(2) _(sqrt(1/2))dx ∫^(1/x)_(0)dy=

= ∫^(sqrt(1/2)) _(0)(2x)dx + ∫^(2) _(sqrt(1/2))(1/x)=

=(x^2)|^(sqrt(1/2)) _(0)+ln|x||^(2) _(sqrt(1/2))=(1/2) - 0 +ln2- ln sqrt(1/2)=

=(1/2)+ln2-ln(2)^(-1/2)=(1/2)+(3/2)ln2

S(квадрата)=2*2=4

p=((1/2)+(3/2)ln2)/4=(1/8)+(3/8)ln2

2)
23979
По формуле геометрической вероятности
р(А)=l/L
L– расстояние от между прямыми
l– расстояние от монеты до прямой.

L=2a; r=a
l=L-2r=2a-2r

p(А)=(2a-2r)/2a=(a-r)/a
О т в е т. (a-r)/a

3.
23975

Так как диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет, то белый цвет занимает половину круга и черный цвет занимает половину круга.

По формуле геометрический вероятности
p=S(белой части)/S(круга)=(1/2)S/S=(1/2)

О т в е т. 1/2=0,5