Линейные уравнения первого порядка

(x+1)y'+y = x^3+x^2, y(0) = 0

y' - 2xy = e^(x^7) * ctg x

y’’+y’tgx=cosx. y(0)=1. y’(0)=0

y'+4xy=2xe^(-x^2)* sqrt(y)

x(y'' + 1) + y' = 0

Определить тип дифференциального уравнения.
Если возможно, то подобрать замену, соответствующую типу уравнения. Замена упростит решение, появится возможность свести исходное уравнение к уравнению с разделяющимися переменными.
Не забудьте вернуться к исходным переменным.
Помните: в результате интегрирования дифференциального уравнения должно получиться семейство функций, зависящих от одной произвольной постоянной С.

Найти общее решение дифференциального уравнения первого порядка.
Подставить в общее решение дифференциального уравнения первого порядка заданные начальные условия, выразив затем константу.
Получить частное решение дифференциального уравнения первого порядка.

(1 - x) · (y' + y) = e^(-x) , y(0) = 0

Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию.

xy' - 2y = 2x⁴, y(1) = 0

y ′ = y + e^x , y(0) = 2 решить дифференциальнoe уравнение

Помогите решить Решить однородное дифференциальное уравнение

Решить линейное дифференциальное уравнение

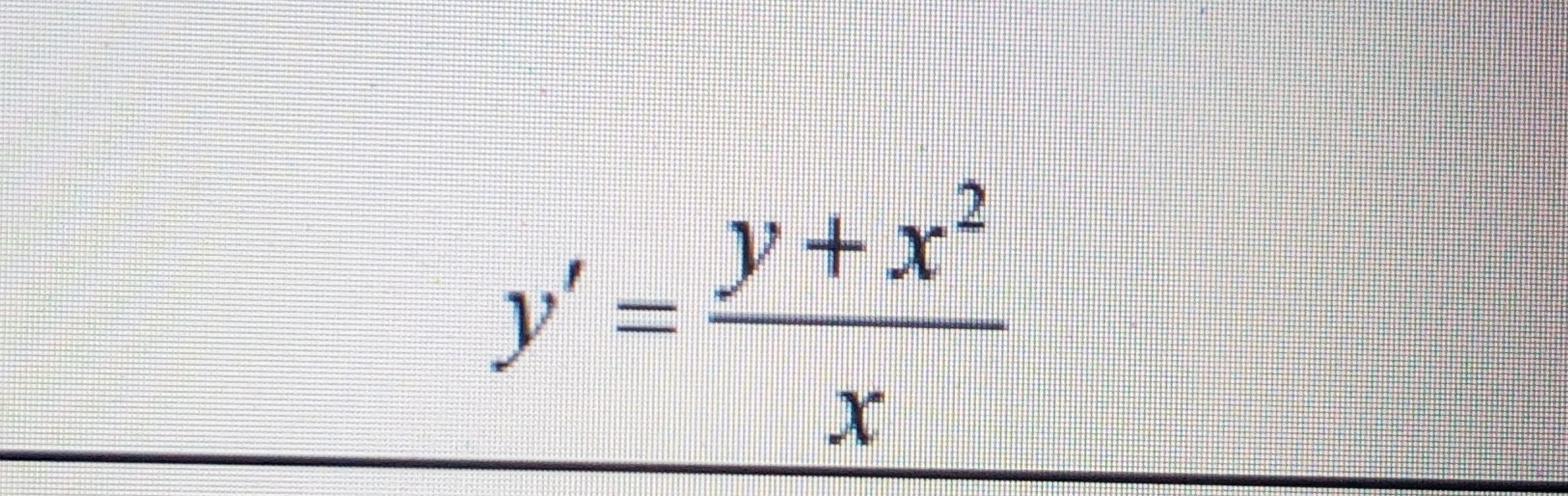
y' - (2/x) y = 2x^3

Помогите пожалуйста Решить линейное дифференциальное уравнение

Помогите пожалуйста Решить однородное дифференциальное уравнение

А) Решить однородное дифференциальное уравнение
Б) Решить линейное уравнение