Задача 8187 ...

NickJackson

27.03.2016

В правильной треугольной пирамиде DABC со стороной основания АВ, равной 30, боковое ребро равно 20. Точки N и М делят рёбра DA и DB в отношении 2:1, считая от вершины D. Плоскость α, содержащая прямую MN, перпендикулярна плоскости основания пирамиды.

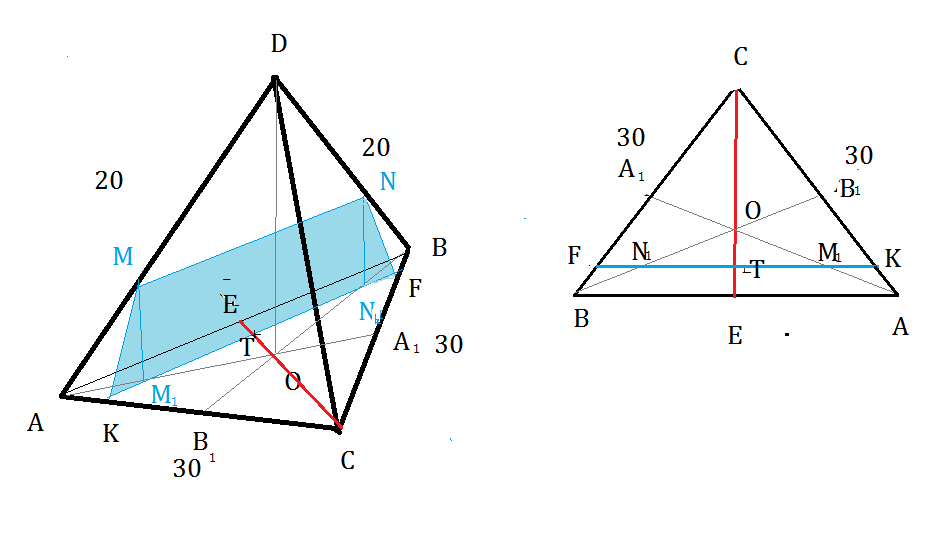
а) Докажите, что плоскость а делит высоту СЕ основания в отношении 8:1, считая от точки С.

б) Найдите площадь сечения пирамиды DABC плоскостью α.

SOVA

28.03.2016

★

В треугольнике АDO проводим ММ1 || SO.
По теореме Фалеcа
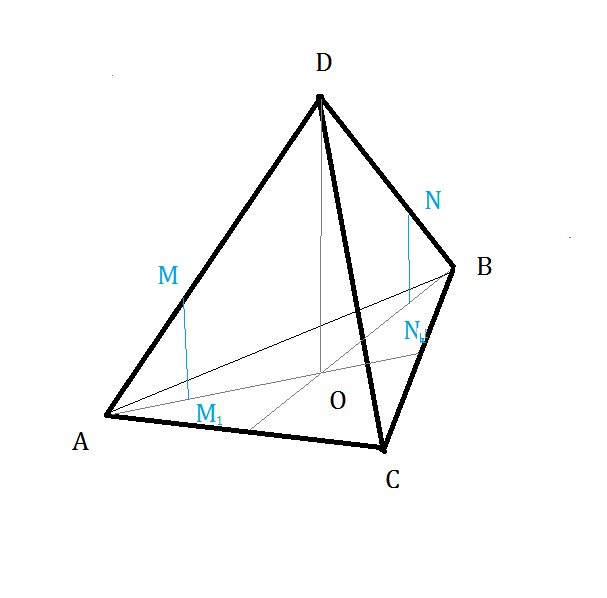
АМ:MD=AM1:OM1=1:2.
В треугольнике BDO проводим NN1 || DO.
По теореме Фалеса
BN1:N1O=1:2.

Треугольник М1ON1 подобен треугольнику АОВ
M1N1:AB=OM1:OA=2:3;
M1N1=30•2:3=20;
AO=BO=CO=R=10√3 (треугольник АВС- правильный)и радиус окружности, описанной около равностороннего треугольника находится по формуле:

R=a√3/3, где а - сторона равностороннего треугольника.

По теореме Пифагора из треугольника ADO:
DO²=AD²-AO²=20²-(10√3)²=400-300=100.
DO=10.

MM1:DO=1:3.
MM1=10/3.

Рассмотрим треугольник BA1A.
A1O=OA/2;
AM1=OA/3 значит ОА=3АМ1
А1О=3АМ1/2
М1А1=M1O+OA1=2AM1+(3AM1/2)=7AM1/2
FM1:АВ=7:9
FM1=210/9
FN1=FM1-M1N1=(210/9)- 20=30/9=10/3
Аналогично
КМ1=10/3
И потому КF=80/3
КF:AB=CT:СE=(80/3):30=8:9
Значит
СТ:ТЕ=8:1
б)S(трапеции FNMK)=(FK+MN)•MM1/2=((80/3)+20)•(10/3)/2=700/9