Задача 8186 Радиус основания конуса равен 4, а...

Julia_Trusova

27.03.2016

Радиус основания конуса равен 4, а высота конуса равна 3sqrt(2). В конусе проведено сечение плоскостью, проходящей через вершину конуса и хорду окружности основания, длина которой равна 4sqrt(2).

а) Докажите, что плоскость, проходящая через середину этой хорды и высоту конуса, перпендикулярна этой хорде.

б) Найдите угол между плоскостью основания и плоскостью сечения.

О-центр основания конуса, DO-высота конуса, DO=3*sqrt(2)
АВ=4*sqrt(2)
△ADB- сечение конуса, проходящей через вершину конуса и хорду окружности основания,
Н-середина АВ.

а)(DOH) - плоскость, проходящая через середину хорды AB и высоту конуса.
△АВО-равнобедренный(АО=ВО=r), ⇒ОН - и медиана, и высота, т.е. АВ⊥ОН
Так как DO-высота, DO⊥AB
Таким образом, АВ ⊥ двум пересекающимся прямым, лежащим в плоскости (DOH), ⇒ АВ ⊥ (DOH).

б)Угол между (ABD) и (АВО) - двугранный угол
ОН ⊥ DB;
DH ⊥ AB (по теореме о трех перпендикулярах)
⇒ ∠DHO-линейный угол двугранного угла между (ABD) и (АВО).
АН=1/2*АВ=1/2*4*sqrt(2)=2*sqrt(2)
Из △АНО по теореме Пифагора:
НО=sqrt(4^2-(2*sqrt(2))^2)=sqrt(16-8)=2*sqrt(2)
Из прямоугольного △НОD: tg∠DHO=DO/OH
tg∠DHO=(3*sqrt(2))/(2*sqrt(2))=3/2
∠DHO=arctg(3/2)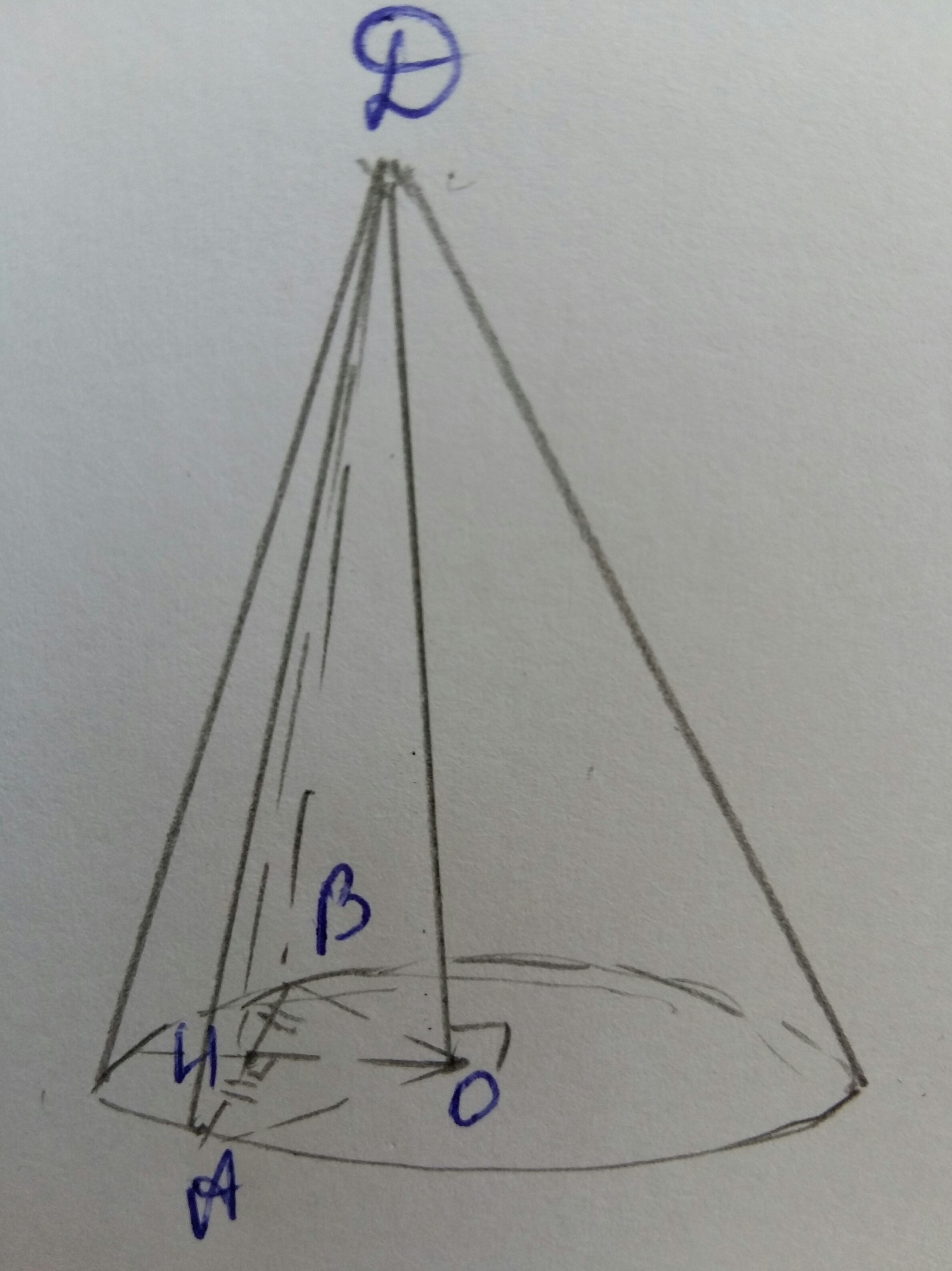

Ответ: arctg(3/2)