Задача 8184 Дан куб ABCDA1B1C1D1 1) Докажите, что...
Условие
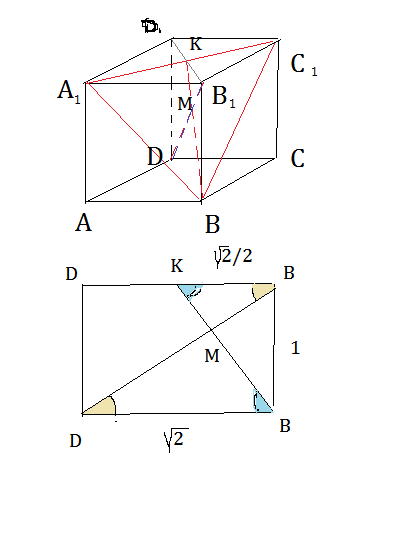
1) Докажите, что прямая B1D перпендикулярна плоскости A1BC1
2) Найдите угол между плоскостями AB1C1 и A1B1C
Решение
Треугольник A1BC1- равносторонний, Проведем высоту ВК (К- точка пересечения диагоналей) B1D пересекается с КВ в точке М.
Треугольники КВ1М и DBM подобны по двум углам. (см. рисунок) D1B1=DB=√2 KB1=√2/2 По теореме Пифагора B1D=√3 KB=√(3/2) KM:MB=1:2 KM:((√3/2)-KB)=1:2 KB=√6/6 B1M:MD=1:2 B1M:(√3- B1M)=1:2 B1M=√3/3
В треугольнике В1КМ B1K²=B1M²+MK² 1/2=(1/3)+(1/6) Треугольник прямоугольный угол B1MK- прямой
Итак, B1D- перпендикулярна двум пересекающимся прямым А1С1 и BK, значит перпендикулярна плоскости А1ВС1.
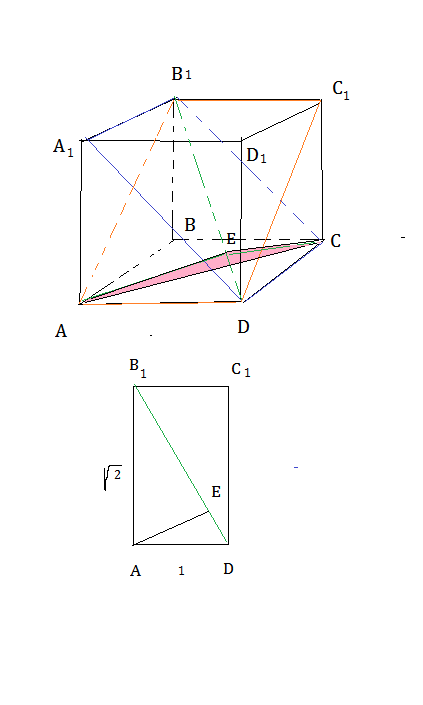
2) Плоскость АВ1С1- это плоскость АB1C1D Плоскость A1B1C- это плоскость A1B1CD
Две эти плоскости имеют общие точки B1 и D. Значит пересекаются по прямой, проходящей через эти точки.
Чтобы построить линейный угол двугранного угла проводим к прямой B1D перпендикуляры AE и EC. AE=EC- высоты прямоугольных треугольников с катетами 1 и √2 и гипотенузой √3 АЕ=ЕС=1•√2/√3=√(2/3)
Из треугольника АСЕ по теореме косинусов АС²=АЕ²+ЕС²-2•АЕ•ЕС•cos ∠AEC (√2)²=(√(2/3))²+(√(2/3))²-2•(√(2/3))•(√(2/3))•cos ∠AEC cos ∠AEC=-1/2 ∠AEC=120°