Задача 8181 Точка E - середина ребра AA1 куба...

Julia_Trusova

27.03.2016

Точка E - середина ребра AA1 куба ABCDA1B1C1D1.

а) Докажите, что сечение куба плоскостью DEB1 является ромбом.
б) Найдите угол между прямыми DE и BD1.

a)Построим сечение куба плоскостью DEB1.
Соединим точки Е и В1, так как они находятся в одной грани, аналогично можно соединить Е и D.
Проведем через точку D прямую, параллельную ЕВ1, F-точка пересечения этой прямой и ребра СС1.
F-середина ребра СС1.
Проведем прямую B1F.(B1F||ED, так как противоположные грани куба параллельны.).
EB1FD - сечение куба плоскостью DEB1.
Так как противоположные стороны у получившегося четырехугольника параллельны, то EB1FD - параллелограмм.
△DAE=△B1A1E=△B1C1F=△DCF по двум катетам
значит, DE=EB1=B1F=FD
⇒ EB1FD-ромб
б)Прямые DE и BD1 скрещивающиеся, угол между скрещивающимися прямыми - это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Проведем прямую параллельную ED через точку D1 в грани АА1D1, E1-точка пересечения этой прямой с прямой АА1.
Угол Е1D1B-искомый угол.
Пусть сторона куба равна х.
Из △EAD по теореме Пифагора: ED=sqrt(x^2+1/4*x^2)=sqrt(5)/2*x
E1D1=ED=sqrt(5)/2*x
Из △ABD по теореме Пифагора: BD=sqrt(x^2+x^2)=sqrt(2)*x
Из △BDD1 по теореме Пифагора: BD1=sqrt(2x^2+x^2)=sqrt(3)*x
Из △ABE1 по теореме Пифагора: BE1=sqrt(x^2+9/4x^2)=sqrt(13)/2*x
По теореме косинусов из △E1D1B:
E1B^2=E1D1^2+BD1^2-2*E1D1*BD1*cos∠E1D1B
13/4*x^2=3*x^2+5/4*x^2-2*sqrt(3)*x*sqrt(5)/2*x*cos∠E1D1B
sqrt(15)*x^2*cos∠E1D1B=17/4*x^2-13/4*x^2
cos∠E1D1B=x^2/(sqrt(15)*x^2)=sqrt(15)/15
∠E1D1B=arccos(sqrt(15)/15)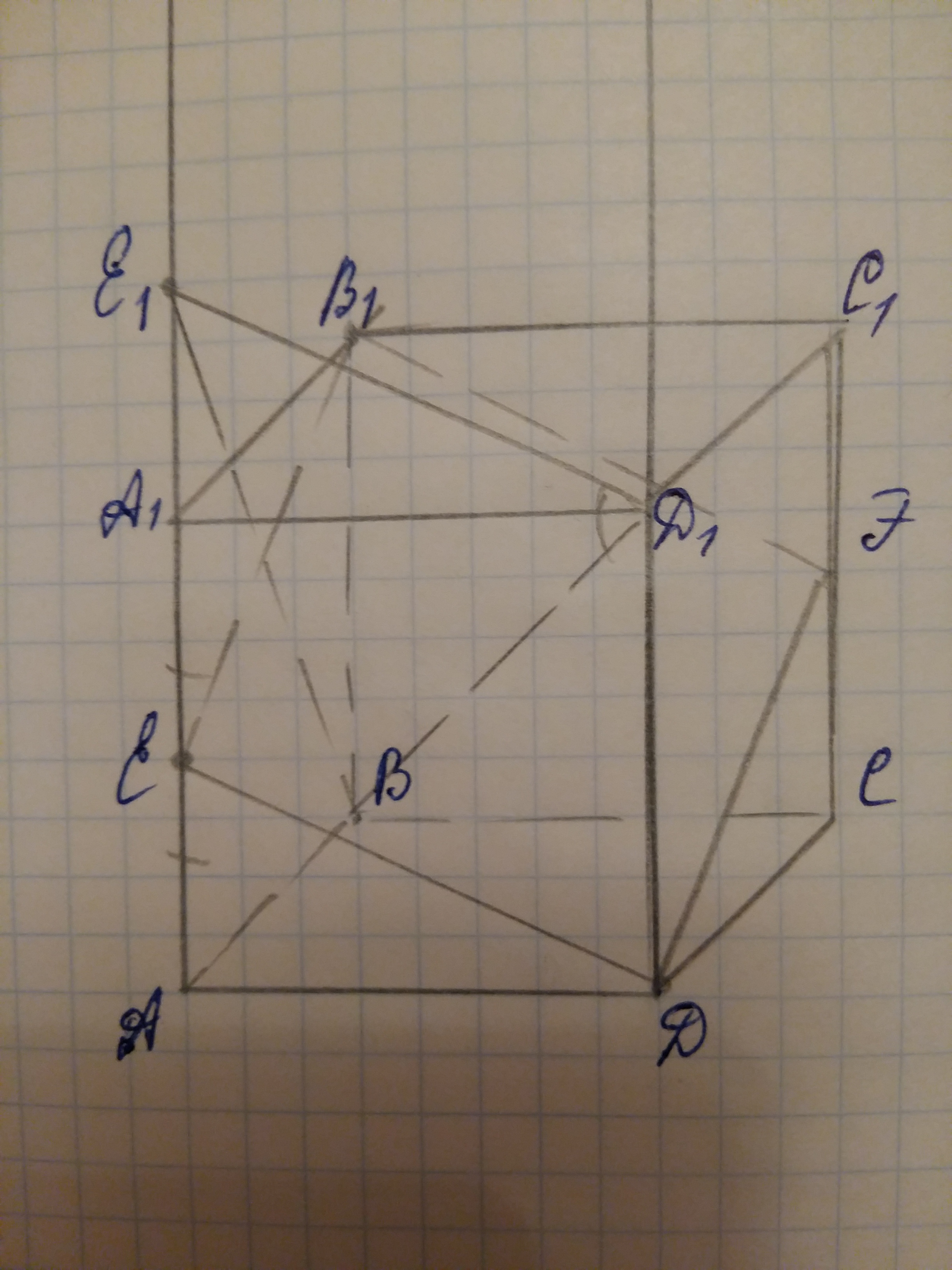

Ответ: arccos(sqrt(15)/15)