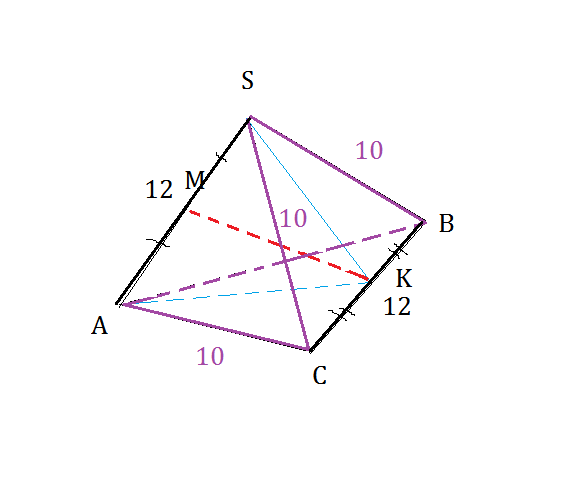
Задача 8161 В пирамиде SABC известны длины ребер...

MariyaNayda

26.03.2016

В пирамиде SABC известны длины ребер AB=AC=SB=SC=10; BC=SA=12. Точка K - середина ребра BC

1) Докажите, что плоскость SAK перпендикулярна плоскости ABC

2) Найдите расстояние между прямыми SA и BC

SOVA

26.03.2016

★

Треугольник SBC и треугольник АВС равные между собой ( по трем сторонам)равнобедренные треугольники
По условию
SC=SB=10 и АВ=АС=10
BC=12-общая сторона.

Высота равнобедренного треугольника, проведенная к основанию является одновременно и медианой.
ВК=СК
SK⊥BC
AK⊥BC

BC - перпендикулярна двум пересекающимся прямым плоскости ASК, значит перпендикулярна плоскости ASK.
Плоскость АВС проходит через прямую ВС (перпендикуляр к другой плоскости), значит плоскость АВС перпендикулярна плоскости ASK
По теореме Пифагора из прямоугольных треугольников
SCK и АСК
SK=8
АК=8

Треугольник SAK - равнобедренный (SK=AK=8)
Высота, проведенная к основанию AS является медианой, делит AS пополам.
КM⊥AS
и
КМ⊥ВС ( ВС ⊥ пл. ASK, значит перпендиулярна любой прямой в этой плоскости, в том числе и КМ).
КМ - расстояние между прямыми AS и ВС.
По теореме Пифагора из прямоугольного треугольника
АМК
d²=KM²=8²-6²=28
d=√28=2√7